如图，在平面直角坐标系中，抛物线 $y=\dfrac{\sqrt3}{3}x^2-\dfrac{2\sqrt 3}{3}x-\sqrt 3$ 与 $x$ 轴交于 $A,B$ 两点（点 $A$ 在点 $B$ 的左侧），与 $y$ 轴交于点 $C$，对称轴于 $x$ 轴交于点 $D$，点 $E\left(4,\dfrac{5\sqrt 3}{3}\right)$ 在抛物线上，点 $P$ 为直线 $CE$ 下方抛物线上的一点，连接 $PC,PE$，当 $\triangle PCE$ 的面积最大时，连接 $CD,CB$，点 $K$ 是线段 $CB$ 的中点，点 $M$ 是 $CP$ 上的一点，点 $N$ 是 $CD$ 上的一点，求 $KM+MN+NK$ 的最小值．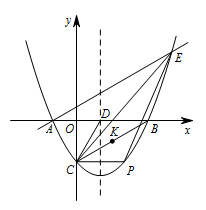
【难度】
【出处】
无
【标注】
【答案】
$3$
【解析】
由已知可得直线 $AE$ 的解析式为 $y=\dfrac {\sqrt 3}{3}x+\dfrac{\sqrt 3}{3}$，
令 $x=0$，得 $y=-\sqrt 3$，所以点 $C(0,-\sqrt 3)$，
所以直线 $CE$ 的解析式为 $y=\dfrac{2\sqrt 3}{3}x-\sqrt 3$，
过点 $P$ 作 $PH\parallel y$ 轴，交 $CE$ 于点 $H$，如图．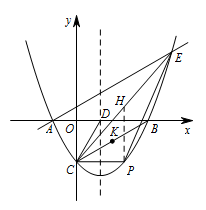
设点 $P$ 的坐标为 $(t,\dfrac{\sqrt3}{3}t^2-\dfrac{2\sqrt 3}{3}t-\sqrt 3)$，则 $H(t,\dfrac {\sqrt 3}{3}t+\dfrac{\sqrt 3}{3})$，
所以 $PH=\dfrac {\sqrt 3}{3}t+\dfrac{\sqrt 3}{3}-(\dfrac{\sqrt3}{3}t^2-\dfrac{2\sqrt 3}{3}t-\sqrt 3)=-\dfrac{\sqrt 3}{3}t^2+\dfrac{4\sqrt 3}{3}t$，
所以 $S_{\triangle PCE}=\dfrac 12|x_E-x_C|\cdot PH=\dfrac 12\times 4\times(-\dfrac{\sqrt 3}{3}t^2+\dfrac{4\sqrt 3}{3}t)=-\dfrac{2\sqrt 3}{3}t^2+\dfrac{8\sqrt 3}{3}t$，
因为 $-\dfrac{2\sqrt 3}{3}<0$，抛物线开口向下，$0<t<4$，
所以当 $t=2$ 时，$S_{\triangle PCE}$ 取最大值，
此时，点 $P$ 为 $(2,-\sqrt 3)$，
因为点 $C(0,-\sqrt 3),B(3,0)$，由三角形中位线定理得 $K(\dfrac 32,-\dfrac{\sqrt 3}{2})$，
因为 $y_C=y_P=-\sqrt 3$，
所以 $PC\parallel x$ 轴，
作 $K$ 关于 $CP$ 的对称点 $K$，
则 $K_1(\dfrac 32,-\dfrac {3\sqrt 3}{2})$，
因为 $\tan\angle OCH=\sqrt 3$，所以 $\angle OCB=60^\circ$，
因为 $D(1,0)$，所以 $\tan\angle OCD=\dfrac{\sqrt 3}{3}$，
所以 $\angle OCD=30^\circ$，
所以 $\angle OCD=\angle DCB=30^\circ$，
所以 $CD$ 平分 $\angle OCB$，
所以点 $K$ 关于 $CD$ 的对称点 $K_2$ 在 $y$ 轴上，
又因为 $CK=OC=\sqrt 3$，所以 $K_2$ 与点 $O$ 重合，
连接 $OK_1$，交 $CD$ 于点 $N$，交 $CP$ 于点 $M$，如图．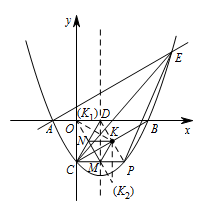
所以 $KM=K_1M,KN=ON$，
所以 $KM+MN+NK=K_1M+MN+ON$，
所以 $K_1K_2=OK_1=3$，
所以所以 $KM+MN+NK$ 的最小值为 $3$．
令 $x=0$，得 $y=-\sqrt 3$，所以点 $C(0,-\sqrt 3)$，
所以直线 $CE$ 的解析式为 $y=\dfrac{2\sqrt 3}{3}x-\sqrt 3$，
过点 $P$ 作 $PH\parallel y$ 轴，交 $CE$ 于点 $H$，如图．
设点 $P$ 的坐标为 $(t,\dfrac{\sqrt3}{3}t^2-\dfrac{2\sqrt 3}{3}t-\sqrt 3)$，则 $H(t,\dfrac {\sqrt 3}{3}t+\dfrac{\sqrt 3}{3})$，所以 $PH=\dfrac {\sqrt 3}{3}t+\dfrac{\sqrt 3}{3}-(\dfrac{\sqrt3}{3}t^2-\dfrac{2\sqrt 3}{3}t-\sqrt 3)=-\dfrac{\sqrt 3}{3}t^2+\dfrac{4\sqrt 3}{3}t$，
所以 $S_{\triangle PCE}=\dfrac 12|x_E-x_C|\cdot PH=\dfrac 12\times 4\times(-\dfrac{\sqrt 3}{3}t^2+\dfrac{4\sqrt 3}{3}t)=-\dfrac{2\sqrt 3}{3}t^2+\dfrac{8\sqrt 3}{3}t$，
因为 $-\dfrac{2\sqrt 3}{3}<0$，抛物线开口向下，$0<t<4$，
所以当 $t=2$ 时，$S_{\triangle PCE}$ 取最大值，
此时，点 $P$ 为 $(2,-\sqrt 3)$，
因为点 $C(0,-\sqrt 3),B(3,0)$，由三角形中位线定理得 $K(\dfrac 32,-\dfrac{\sqrt 3}{2})$，
因为 $y_C=y_P=-\sqrt 3$，
所以 $PC\parallel x$ 轴，
作 $K$ 关于 $CP$ 的对称点 $K$，
则 $K_1(\dfrac 32,-\dfrac {3\sqrt 3}{2})$，
因为 $\tan\angle OCH=\sqrt 3$，所以 $\angle OCB=60^\circ$，
因为 $D(1,0)$，所以 $\tan\angle OCD=\dfrac{\sqrt 3}{3}$，
所以 $\angle OCD=30^\circ$，
所以 $\angle OCD=\angle DCB=30^\circ$，
所以 $CD$ 平分 $\angle OCB$，
所以点 $K$ 关于 $CD$ 的对称点 $K_2$ 在 $y$ 轴上，
又因为 $CK=OC=\sqrt 3$，所以 $K_2$ 与点 $O$ 重合，
连接 $OK_1$，交 $CD$ 于点 $N$，交 $CP$ 于点 $M$，如图．
所以 $KM=K_1M,KN=ON$，所以 $KM+MN+NK=K_1M+MN+ON$，
所以 $K_1K_2=OK_1=3$，
所以所以 $KM+MN+NK$ 的最小值为 $3$．
答案
解析
备注
