如图，直线 $y=\dfrac 34x+3$ 分别与 $x$ 轴，$y$ 轴交于点 $A,B$，抛物线 $y=-x^2+2x+1$ 与 $y$ 轴交于点 $C$．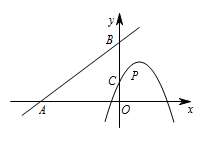
【难度】
【出处】
无
【标注】
-
若点 $P(x,y)$ 是抛物线 $y=-x^2+2x+1$ 上的任意一点，设点 $P$ 到直线 $AB$ 的距离为 $d$，求 $d$ 关于 $x$ 的函数解析式，并求 $d$ 取最小值时点 $P$ 的坐标；标注答案$d=\dfrac45x^2-x+\dfrac 85$，$P\left(\dfrac 58,\dfrac{119}{64}\right)$解析过点 $P$ 作 $PH\perp AB$ 于点 $H$，过点 $H$ 作 $x$ 轴的平行线 $MN$，分别过点 $A,P$ 作 $MN$ 的垂线段，垂足分别为 $M,N$．
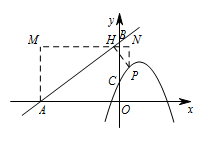设 $H(m,\dfrac 34m+3)$，则 $M(-4,\dfrac 34m+3)$，$N(x,\dfrac 34m+3)$，$P(x,-x^2+2x+1)$，
因为 $PH\perp AB$，所以 $\angle CHN+\angle AHM=90^\circ$，
因为 $AM\perp MN$，所以 $\angle MAH+\angle AHM=90^\circ$，
所以 $\angle MAH=\angle CHN$，
因为 $\angle AMH=\angle CNH=90^\circ$，
所以 $\triangle AMH\cong \triangle HNP$，
因为 $MN\parallel y$ 轴，所以 $\triangle MAH\backsim \triangle OBA$，
所以 $\triangle OBA\backsim \triangle NHP$，
所以 $\dfrac{NH}{3}=\dfrac{CN}{4}=\dfrac{CH}{5}$，
所以 $\dfrac{x-m}{3}=\dfrac{(\dfrac 34m+3)-(-x^2+2x+1)}{4}=\dfrac{d}{5}$，
整理得：$d=\dfrac45x^2-x+\dfrac 85$，所以当 $x=\dfrac 58$，即 $P\left(\dfrac 58,\dfrac{119}{64}\right)$． -
若点 $E$ 在抛物线 $y=-x^2+2x+1$ 的对称轴上移动，点 $F$ 在直线 $AB$ 上移动，求 $CE+EF$ 的最小值．标注答案$\dfrac{14}{5}$解析作点 $C$ 关于对称轴 $x=1$ 的对称点 $C'$，则 $C'(2,1)$．
过点 $C'$ 作 $C'F\perp AB$ 于点 $F$，且与对称轴交于点 $E$，此时 $FC'$ 的长为 $ CE+EF $ 的最小值．
连接 $C'B,C'A$，作 $C'K\perp x$ 轴于点 $K$．
则 $S_{\triangle ABC'}=S_{\triangle ABO}+S_{\text{梯形}C'KOB}-S_{\triangle C'KA}$，
所以 $FC'=\dfrac{14}{5}$，则 $CE+EF$ 的最小值是 $\dfrac{14}{5}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
