在平面直角坐标系中，抛物线 $y=-x^2-2x+3$ 与 $x$ 轴交于 $A$，$B$ 两点（$A$ 在 $B$ 的左侧），与 $y$ 轴交于点 $C$，顶点为 $D$．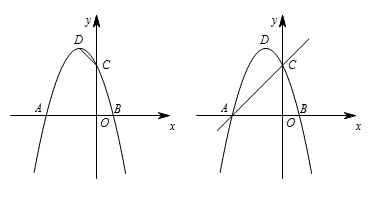
【难度】
【出处】
无
【标注】
-
如图1，在 $x$ 轴上找一点 $E$，使得 $\triangle CDE$ 的周长最小，求点 $E$ 的坐标；标注答案$\left(-\dfrac 37,0\right)$解析作点 $C(0,3)$ 关于 $x$ 轴的对称点 $C'$，则 $C'$ 的坐标为 $(0,-3)$．连接 $DC'$，$DC'$ 交 $x$ 轴于点 $E$，则点 $E$ 就是使得 $\triangle CDE$ 的周长最小的点，如图所示．
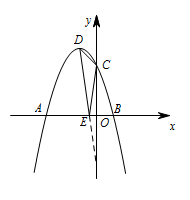设直线 $DC'$ 的解析式为 $y=kx+b$，
把 $D(-1,4)$，$C'(0,-3)$ 分别代入 $y=kx+b$，得
$\begin{cases}4=-k+b,\\-3=b.\end{cases}$ 解得 $\begin{cases}k=-7,\\b=-3.\end{cases}$
所以直线 $DC'$ 的解析式为 $y=-7x-3$．
把 $y=0$ 代入 $y=-7x-3$，得 $0=-7x-3$．解得 $x=-\dfrac 37$．
所以点 $E$ 的坐标为 $\left(-\dfrac 37,0\right)$． -
如图2，$F$ 为直线 $AC$ 上的动点，在抛物线上是否存在点 $P$，使得 $\triangle AFP$ 为等腰直角三角形？若存在，求出点 $P$ 的坐标；若不存在，请说明理由．标注答案点 $P$ 的坐标为 $(2,-5)$ 或 $(1,0)$解析存在符合题意的点 $P$．
设直线 $AC$ 的解析式为 $y=ax+c$，把 $A(-3,0)$，$C(0,3)$ 分别代入 $y=ax+c$，得
$\begin{cases}-3a+c=0,\\c=3.\end{cases}$ 解得 $\begin{cases}a=1,\\c=3.\end{cases}$
所以直线 $AC$ 的解析式为 $y=x+3$．
设点 $F$ 的坐标为 $(m,m+3)$．
① 当 $\angle PAF=90^\circ$ 时，$P$ 的坐标为 $(m,-m-3)$．
把 $P(m,-m-3)$ 代入 $y=-x^2-2x+3$，得
$-m-3=-m^2-2m+3$．
解得 $m_1=-3$（不合题意，舍去），$m_2=2$．
所以 $P$ 的坐标为 $(2,-5)$．
② 当 $\angle AFP=90^\circ$ 时，$P$ 的坐标为 $(2m+3,0)$．
把 $P(2m+3,0)$ 代入 $y=-x^2-2x+3$，得
$-(2m+3)^2-2(2m+3)+3=0$．
解得 $m_1=-3$（不合题意，舍去），$m_2=-1$．
所以 $P$ 的坐标为 $(1,0)$．
③ 当 $\angle APF=90^\circ$ 时，$P$ 的坐标为 $(m,0)$．
把 $P(m,0)$ 代入 $y=-x^2-2x+3$，得
$-m^2-2m+3=0$．
解得 $m_1=-3$（不合题意，舍去），$m_2=1$．
所以 $P$ 的坐标为 $(1,0)$．
综上可知，符合题意的点 $P$ 的坐标为 $(2,-5)$ 或 $(1,0)$．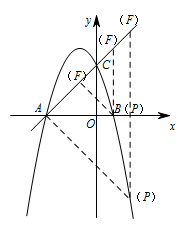
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
