如图,抛物线 $y=ax^2+bx-4$($a\ne 0$)与 $x$ 轴交于 $A(4,0),B(-1,0)$ 两点,过点 $A$ 的直线 $y=-x+4$ 交抛物线于点 $C$.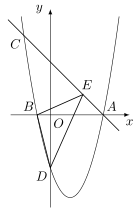

【难度】
【出处】
无
【标注】
-
在直线 $AC$ 上有一动点 $E$,当点 $E$ 在某个位置时,使 $\triangle BDE$ 的周长最小,求此时 $E$ 点坐标;标注答案$E\left(\dfrac{32}{13} ,\dfrac{20}{13}\right)$解析因为抛物线 $y=ax^2+bx-4$($a\ne0$)与 $x$ 轴交于 $A(4,0),B(-1,0)$ 两点,
所以 $\begin{cases}16a+4b-4=0,\\ a-b-4=0.\end{cases}$
所以 $\begin{cases}a=1,\\b=-3.\end{cases}$
所以抛物线解析式为 $y=x^2-3x-4$,
所以点 $D(0,-4)$.
因为点 $C$ 是直线 $y=-x+4$ 与抛物线的交点,
所以联立解得 $\begin{cases}x=4,\\y=0.\end{cases}$(舍)或 $\begin{cases}x=-2,\\y=6.\end{cases}$
所以 $C(-2,6)$,
因为 $A(4,0)$,
所以直线 $AC$ 解析式为 $y=-x+4$,
如图,作点 $B$ 关于直线 $AC$ 的对称点 $F$,连接 $BF$ 交 $AC$ 于点 $G$,连接 $DF$ 交 $AC$ 于点 $E$.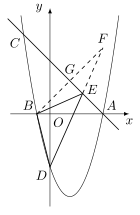 因为直线 $BF\perp AC$,且点 $B(-1,0)$,
因为直线 $BF\perp AC$,且点 $B(-1,0)$,
所以直线 $BF$ 解析式为 $y=x+1$.
设点 $F(m,m+1)$,所以 $G\left(\dfrac{m-1}{2} ,\dfrac{m+1}{2}\right)$.
因为点 $G$ 在直线 $AC$ 上,
所以 $-\dfrac{m-1}{2}+4=\dfrac{m+1}{2}$,即 $m=4$,
所以点 $F(4,5)$.
因为点 $D(0,-4)$,
所以直线 $DF$ 解析式为 $y=\dfrac 94 x-4$.
因为直线 $AC$ 解析式为 $y=-x+4$,
所以直线 $DF$ 和直线 $AC$ 的交点 $E\left(\dfrac{32}{13} ,\dfrac{20}{13}\right)$. -
当动点 $E$ 在直线 $AC$ 与抛物线围成的封闭线 $A-C-B-D-A$ 上运动时,是否存在使 $\triangle BDE$ 为直角三角形的情况,若存在,请直接写出符合要求的 $E$ 点的坐标;若不存在,请说明理由.标注答案满足条件的点 $E$ 的坐标为 $E(3,1)$ 或 $\left(\dfrac{13}{4} ,-\dfrac{51}{16}\right)$解析因为 $BD=\sqrt{17}$,
由第1问可得点 $B$ 到线段 $AC$ 的距离为 $BG=\dfrac 12 BF=\dfrac 12 \times5\sqrt 2 =\dfrac{5\sqrt 2}{2} >BD$,
所以 $\angle BED$ 不可能是直角.
因为点 $B(-1,0)$,点 $D(0,-4)$,
所以直线 $BD$ 解析式为 $y=-4x+4$.
$\triangle BDE$ 为直角三角形分为两种情况:
① 当 $\angle BDE=90^\circ$ 时,$BE\perp BD$ 交 $AC$ 于 $B$,
所以直线 $BE$ 解析式为 $y=\dfrac 14 x+\dfrac 14$.
因为点 $E$ 在直线 $AC$:$y=-x+4$ 的图象上,
所以点 $E(3,1)$;
② 当 $\angle BDE=90^\circ$ 时,$BE\perp BD$ 交 $AC$ 于 $D$,
所以直线 $BE$ 的解析式为 $y=\dfrac 14 x-4$.
因为点 $E$ 在抛物线 $y=x^2-3x-4$ 上,
所以直线 $BE$ 与抛物线的交点为 $(0,-4)$ 和 $\left(\dfrac{13}{4} ,-\dfrac{51}{16}\right)$
所以点 $E\left(\dfrac{13}{4} ,-\dfrac{51}{16}\right)$.
即满足条件的点 $E$ 的坐标为 $E(3,1)$ 或 $\left(\dfrac{13}{4} ,-\dfrac{51}{16}\right)$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2