如图，直线 $y=-3x+3$ 与 $x$ 轴、$y$ 轴分别交于点 $A,B$．抛物线 $y=a\left(x-2\right)^2+k$ 经过 $A,B$，并与 $x$ 轴交于另一点 $C$，其顶点为 $P$．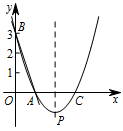
【难度】
【出处】
无
【标注】
-
在图中求一点 $Q,A,B,C$ 为顶点的四边形是平行四边形，请直接写出相应的点 $Q$ 的坐标；标注答案$Q$ 点的坐标为 $\left(-2,3\right)$ 或 $\left(2,3\right)$ 或 $\left(4,-3\right)$解析由直线解析式可得点 $A\left(1,0\right)$，点 $B\left(0,3\right)$．
而抛物线的对称轴为 $x=2$，所以点 $C(3,0)$．
所以 $AC=3-1=2$，$AB=\sqrt {10}$．
① 如图，过点 $B$ 作平行 $x$ 轴的直线，在 $B$ 点两侧分别截取线段 $BQ_1=BQ_2=AC=2$．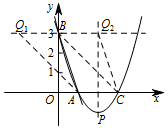
则点 $Q_1\left(-2,3\right)$，点 $Q_2\left(2,3\right)$，
此时四边形 $ACBQ_1$ 和四边形 $ACQ_2B$ 均为平行四边形．
② 如图，过点 $C$ 作 $AB$ 的平行线，在 $C$ 点分别两侧截取 $CQ_3=CQ_4=AB= \sqrt {10}$．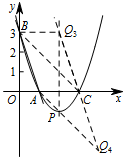
则点 $Q_3,Q_4$ 到 $x$ 轴的距离都等于点 $B$ 到 $x$ 轴的距离也为 $3$，且到直线 $x=3$ 的距离为 $1$，
所以点 $ Q_3\left(2,3\right)$，点 $Q_4\left(4,-3\right)$．
而此时四边形 $ACQ_3B$ 和四边形 $AQ_4CB$ 也为平行四边形．
综上所述，满足条件的点 $Q$ 的坐标为 $\left(-2,3\right)$ 或 $\left(2,3\right)$ 或 $\left(4,-3\right)$． -
抛物线的对称轴上是否存在一点 $M$，使 $\triangle ABM$ 的周长最小？若存在，求 $\triangle ABM$ 的周长；若不存在，请说明理由；标注答案存在，$\triangle ABM$ 的周长为 $\sqrt {10}+3\sqrt 2$解析如图，连接 $BC$ 交对称轴于点 $M$，连接 $MA$．
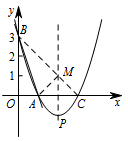此时 $\triangle ABM$ 周长最小，最小值为 $AB+BC$．
易求 $AB=\sqrt{10}$，$BC=3\sqrt 2$，
所以 $\triangle ABM$ 的周长的最小值为 $\sqrt {10}+3\sqrt 2$． -
抛物线的对称轴是上是否存在一点 $N$，使 $\triangle ABN$ 是以 $AB$ 为斜边的直角三角形？若存在，求出 $N$ 点的坐标，若不存在，请说明理由．标注答案存在，点 $N$ 的坐标为 $\left(2,1\right)$ 或 $\left(2,2\right)$解析设点 $N$ 的坐标为 $\left(2,n\right)$，
则 $NB^2=2^2+\left(n-3\right)^2=n^2-6n+13$，$NA^2=\left(2-1\right)^2+n^2=1+n^2$，且 $AB^2=10$．
当 $\triangle ABN$ 为以 $AB$ 为斜边的直角三角形时，由勾股定理可得 $NB^2+NA^2=AB^2$，
所以 $ n^2-6n+13+1+n^2=10$，解得 $n=1$ 或 $n=2$，
即点 $N$ 的坐标为 $\left(2,1\right)$ 或 $\left(2,2\right)$，
综上所述，存在满足条件的 $N$ 点，其坐标为 $\left(2,1\right)$ 或 $\left(2,2\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
