已知 $\triangle ABC$ 的外接圆圆心为 $O$，且 $\angle A=60^\circ$，若 $\overrightarrow{AO}=\alpha\overrightarrow{AB}+\beta\overrightarrow{AC}(\alpha,\beta\in\mathbb R)$，则 $\alpha+\beta$ 的最大值为 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
C
【解析】
如图，圆 $O$ 为 $\triangle ABC$ 的外接圆，设半径为 $2$，则 $OE=1$，其中 $E$ 为 $BC$ 中点．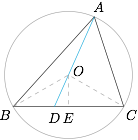
延长 $AO$ 交直线 $BC$ 与点 $D$，则$$\overrightarrow{AO}=\lambda\overrightarrow{AD}=\alpha\overrightarrow{AB}+\beta\overrightarrow{AC},$$整理得$$\overrightarrow{AD}=\dfrac{\alpha}{\lambda}\overrightarrow{AB}+\dfrac{\beta}{\lambda}\overrightarrow{AC},$$结合三点共线的向量表达，由于 $B,C,D$ 共线，于是 $\lambda=\alpha+\beta$，又$$\lambda=\dfrac{AO}{AD}=\dfrac{AO}{AO+OD}\leqslant\dfrac{AO}{AO+OE}=\dfrac23,$$当且仅当 $D$ 与 $E$ 重合时，等号成立，因此 $\alpha+\beta$ 的最大值为 $\dfrac23$．
延长 $AO$ 交直线 $BC$ 与点 $D$，则$$\overrightarrow{AO}=\lambda\overrightarrow{AD}=\alpha\overrightarrow{AB}+\beta\overrightarrow{AC},$$整理得$$\overrightarrow{AD}=\dfrac{\alpha}{\lambda}\overrightarrow{AB}+\dfrac{\beta}{\lambda}\overrightarrow{AC},$$结合三点共线的向量表达，由于 $B,C,D$ 共线，于是 $\lambda=\alpha+\beta$，又$$\lambda=\dfrac{AO}{AD}=\dfrac{AO}{AO+OD}\leqslant\dfrac{AO}{AO+OE}=\dfrac23,$$当且仅当 $D$ 与 $E$ 重合时，等号成立，因此 $\alpha+\beta$ 的最大值为 $\dfrac23$．
题目
答案
解析
备注
