以平面上一点 $O$ 为直角顶点，分别画出两个直角三角形，记作 $\triangle AOB$ 和 $\triangle COD$，其中 $ \angle ABO=30^\circ$．如图，若 $BO=3\sqrt3$，点 $N$ 在线段 $OD$ 上，且 $NO=2$，点 $P$ 是线段 $AB$ 上的一个动点，在将 $\triangle AOB$ 绕点 $O$ 旋转的过程中，求线段 $PN$ 最小值和最大值．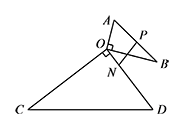
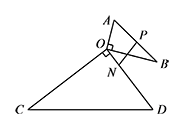
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
过 $O$ 作 $OE\perp AB$ 于 $E$，则 $OE=\dfrac 12 OB=\dfrac{3\sqrt3}{2}$．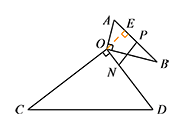
故当 $P$ 在点 $E$ 处时，$OP$ 长度取最小值 $\dfrac{3\sqrt3}{2}$；当 $P$ 在点 $B$ 处时，$OP$ 长度取最大值 $3\sqrt3$．
① 当 $\triangle AOB$ 绕点 $O$ 旋转到 $O,E,D$ 三点共线，且点 $E$ 在线段 $OD$ 上时，$NP$ 取最小值 $OE-ON=\dfrac{3\sqrt3}{2}-2$；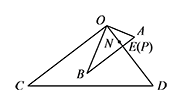
② 当 $\triangle AOB$ 绕点 $O$ 旋转到 $O,B,D$ 三点共线，且点 $B$ 在线段 $DO$ 的延长线上时，$NP$ 取最大值 $OB+ON=3\sqrt3+2$．
所以线段 $PN$ 长度的最小值为 $\dfrac {3}{2}\sqrt3-2$，最大值为 $3\sqrt3+2$．
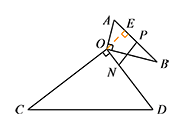故当 $P$ 在点 $E$ 处时，$OP$ 长度取最小值 $\dfrac{3\sqrt3}{2}$；当 $P$ 在点 $B$ 处时，$OP$ 长度取最大值 $3\sqrt3$．① 当 $\triangle AOB$ 绕点 $O$ 旋转到 $O,E,D$ 三点共线，且点 $E$ 在线段 $OD$ 上时，$NP$ 取最小值 $OE-ON=\dfrac{3\sqrt3}{2}-2$；
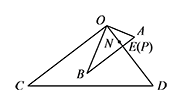② 当 $\triangle AOB$ 绕点 $O$ 旋转到 $O,B,D$ 三点共线，且点 $B$ 在线段 $DO$ 的延长线上时，$NP$ 取最大值 $OB+ON=3\sqrt3+2$．所以线段 $PN$ 长度的最小值为 $\dfrac {3}{2}\sqrt3-2$，最大值为 $3\sqrt3+2$．
答案
解析
备注
