已知正方形 $ABCD$ 的边长为 $1$，点 $P$ 为正方形内一动点，若点 $M$ 在 $AB$ 延长线上，且满足 $\triangle PBC \backsim \triangle PAM$，延长 $BP$ 交 $AD$ 于点 $N$，连接 $CM$，是否存在满足条件的点 $P$，使得 $PC=\dfrac 12$？请说明理由．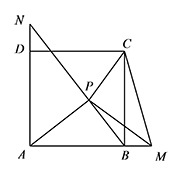
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
因为 $\triangle PBC \backsim \triangle PAM$，
所以 $\angle ABP+\angle PAM=\angle ABP+\angle PBC=90^\circ$，
所以 $AP\perp BN$．
从而 $\dfrac{AB}{AN}=\dfrac{PB}{PA}=\dfrac{BC}{AM}$，
所以 $AM=AN$．
如图，以 $AB$ 为直径作半圆 $O$，则点 $P$ 半圆上．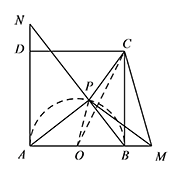
连接 $OC,OP$，则 $OP+PC\geqslant OC$，
而 $OP=\dfrac 12$，$OC=\dfrac{\sqrt 5}2$，
所以 $PC\geqslant \dfrac{\sqrt 5-1}{2}$，
故不存在满足条件的点 $P$，使得 $PC=\dfrac 12$．
所以 $\angle ABP+\angle PAM=\angle ABP+\angle PBC=90^\circ$，
所以 $AP\perp BN$．
从而 $\dfrac{AB}{AN}=\dfrac{PB}{PA}=\dfrac{BC}{AM}$，
所以 $AM=AN$．
如图，以 $AB$ 为直径作半圆 $O$，则点 $P$ 半圆上．
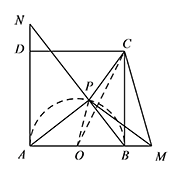连接 $OC,OP$，则 $OP+PC\geqslant OC$，而 $OP=\dfrac 12$，$OC=\dfrac{\sqrt 5}2$，
所以 $PC\geqslant \dfrac{\sqrt 5-1}{2}$，
故不存在满足条件的点 $P$，使得 $PC=\dfrac 12$．
答案
解析
备注
