问题如图1，点 $A$ 为线段 $BC$ 外一动点，且 $BC=b$，$AB=a$．当点 $A$ 位于 $CB$ 的延长线上时线段 $AC$ 的长取得最大值，且最大值为 $a+b$．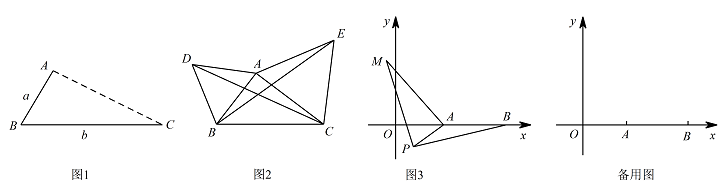
【难度】
【出处】
无
【标注】
-
应用：点 $A$ 为线段 $BC$ 外一动点，且 $BC=3$，$AB=1$．如图2所示，分别以 $AB,AC$ 为边，作等边三角形 $ABD$ 和等边三角形 $ACE$，连接 $CD,BE$．
（i）请找出图中与 $BE$ 相等的线段，并说明理由；
（ii）直接写出线段 $BE$ 长的最大值．标注答案（i）$DC=BE$，
（ii）$BE$ 长的最大值是 $4$解析（i）因为 $\triangle ABD$ 和 $\triangle ACE$ 都是等边三角形，
所以 $ AD=AB$，$AC=AE$，$\angle BAD=\angle CAE=60^\circ$，
所以 $\angle BAD+\angle BAC=\angle CAE+\angle BAC$，即 $\angle CAD=\angle EAB$，
所以 $\triangle CAD\cong\triangle EAB\left(\mathrm {SAS}\right)$．
所以 $ DC=BE$．
（ii）$BE$ 长的最大值是 $4$． -
拓展：如图3，在平面直角坐标系中，点 $A$ 的坐标为 $\left(2,0\right)$，点 $B$ 的坐标为 $\left(5,0\right)$，点 $P$ 为线段 $AB$ 外一动点，且 $PA=2$，$PM=PB$，$\angle BPM=90^\circ$．请直接写出线段 $AM$ 长的最大值及此时点 $P$ 的坐标．标注答案$AM$ 的最大值为 $3+2\sqrt 2$，点 $P$ 的坐标为 $\left(2-\sqrt 2,\sqrt 2\right)$解析如图，构造 $\triangle BNP\cong\triangle MAP$，则 $NB=AM$．
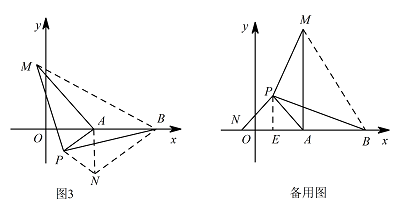由第1问知，当点 $N$ 在 $BA$ 的延长线上时，$NB$ 有最大值（如备用图）．
易得 $\triangle APN$ 是等腰直角三角形，$AP=2$，
所以 $AN=2\sqrt 2$，
所以 $AM=NB=AB+AN=3+2\sqrt 2$．
过点 $P$ 作 $PE\perp x$ 轴于点 $E$，$PE=AE=\sqrt 2$，
又 $A\left(2,0\right)$，
所以 $P\left(2-\sqrt 2,\sqrt 2\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
