• 题型

  >

  几何部分

  >

  线段最值

  >

  轴对称之最短路径

$ M\left(\dfrac{3}{2},\dfrac{13}{4}\right)$

将点 $B\left(1,4\right)$，$E\left(3,0\right)$ 的坐标代入抛物线的解析式得 $\begin{cases}a+b=4,\\9a+3b=0,\end{cases}$
解得 $\begin{cases}a=-2,\\b=6,\end{cases}$
抛物线的解析式为 $y=-2x^2+6x$．
因为 $ BD\perp DE$，所以 $\angle BDE=90^\circ $，
所以 $\angle BDC+\angle EDO=90^\circ $．
又因为 $\angle ODE+\angle DEO=90^\circ $，
所以 $ \angle BDC=\angle DEO$．
在 $\triangle BDC$ 和 $\triangle DOE$ 中
$\begin{cases}\angle BCD=\angle DOE=90^{\circ},\\ \angle BDC=\angle DEO,\\ DB=DE,\end{cases}$
所以 $ \triangle BDC\cong \triangle DE O$，
所以 $ OD=AO=1$，
所以 $D\left(0,1\right)$．
如图所示作点 $B$ 关于抛物线的对称轴的对称点 $B'$，连接 $B'D$ 交抛物线的对称轴与点 $M$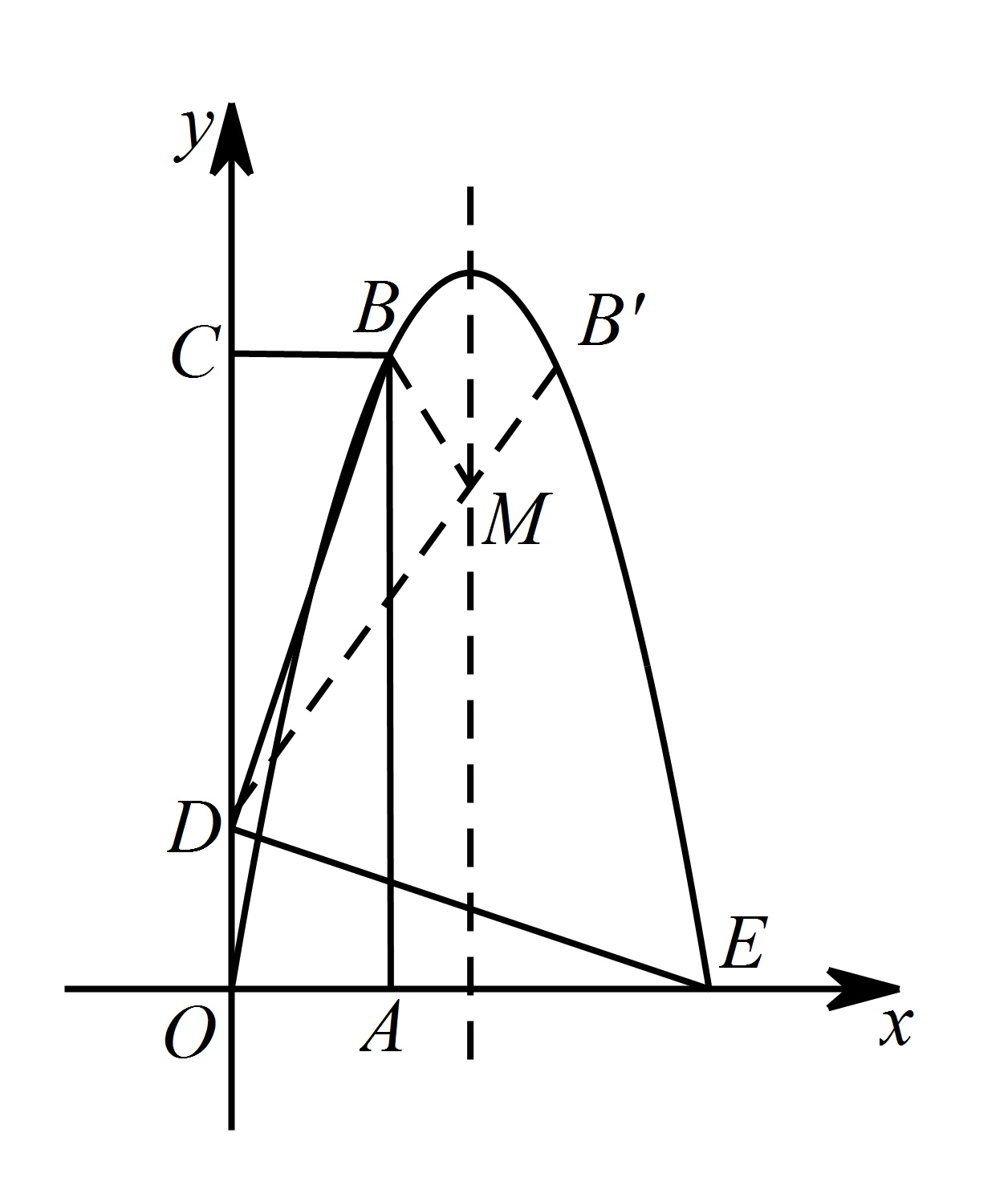．因为 $ x=-\dfrac{b}{2a}=\dfrac{3}{2}$，
所以点 $B'$ 的坐标为 $\left(2,4\right)$．
因为点 $B$ 与点 $B'$ 关于 $x=\dfrac{3}{2}$ 对称，
所以 $ MB=B'M$，
所以 $DM+MB=DM+MB'$．
所以当点 $D$，$M$，$B'$ 在一条直线上时，$MD+MB$ 有最小值（即 $\triangle BMD$ 的周长有最小值）．
因为由两点间的距离公式可知：$BD=\sqrt{1^2+\left(4-1\right)^2}=\sqrt{10}$，$DB'=\sqrt{2^2+\left(4-1\right)^2}=\sqrt{13}$，
所以 $\triangle BDM的最小值=\sqrt{10}+\sqrt{13}$．
设直线 $B'D$ 的解析式为 $y=kx+b$．
将点 $D$，$B'$ 的坐标代入得：$\begin{cases}b=1,\\2k+b=4,\end{cases}$
解得 $k=\dfrac{3}{2}$，$b=1$．
所以直线 $DB'$ 的解析式为 $y=\dfrac{3}{2}x+1$．
将 $x=\dfrac{3}{2}$ 代入得 $y=\dfrac{13}{4}$．
所以 $ M\left(\dfrac{3}{2},\dfrac{13}{4}\right)$

• 题型

  >

  代几综合

  >

  函数与面积

$\left(\dfrac{7}{4},\dfrac{35}{8}\right)$

如图，过点 $F$ 作 $FG\perp x$ 轴，垂足为点 $G$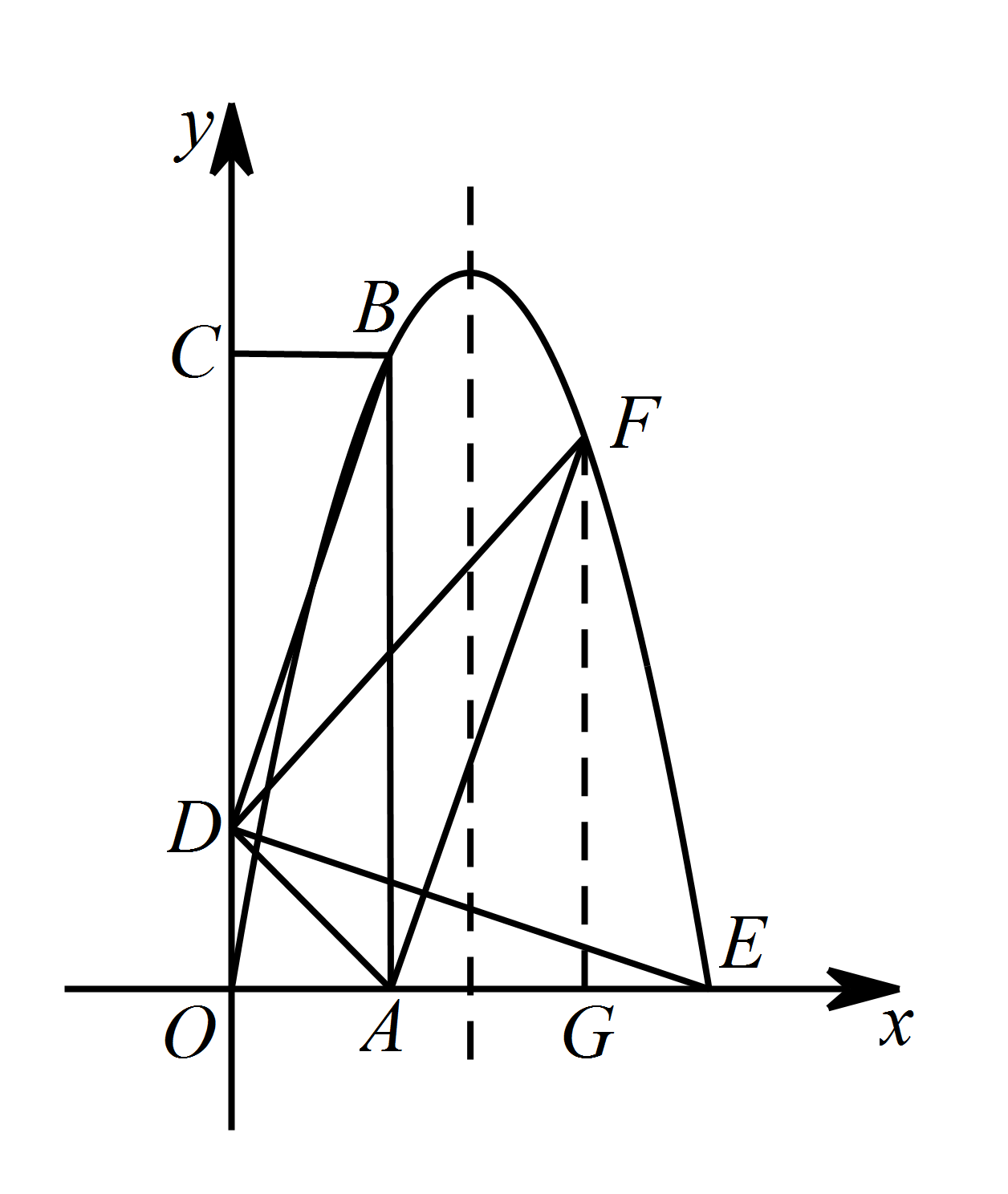．设点 $F\left(a,-2a^2+6a\right)$，则 $OG=a$，$FG=-2a^2+6a$．
因为 $ S_{梯形DOGF}=\dfrac{1}{2}\left(OD+FG\right)\cdot OG=\dfrac{1}{2}\left(-2a^2+6a+1\right)\times a=-a^3+3a^2+\dfrac{1}{2}a$，$S_{\triangle ODA}=\dfrac{1}{2}OD\cdot OA=\dfrac{1}{2}\times 1\times 1=\dfrac{1}{2}$，$S_{\triangle AGF}=\dfrac{1}{2}AG\cdot FG=-a^3+4a^2-3a$，
所以 $ S_{\triangle FDA}=S_{梯形DOGF}-S_{\triangle ODA}-S_{\triangle AGF}=-a^2+\dfrac{7}{2}a-\dfrac{1}{2}$．
所以当 $a=\dfrac{7}{4}$ 时，$S_{\triangle FDA}$ 的最大值为 $\dfrac{41}{16}$．
所以点 $F$ 的坐标为 $\left(\dfrac{7}{4},\dfrac{35}{8}\right)$．