如图1，点 $O$ 是正方形 $ABCD$ 两对角线的交点，延长 $OD$ 到点 $G$，延长 $OC$ 到点 $E$，使 $OG=2OD$，$OE=2OC$，然后以 $OG,OE$ 为邻边作正方形 $OEFG$，连接 $AG,DE$．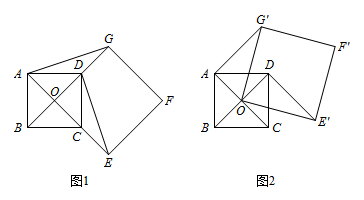
【难度】
【出处】
无
【标注】
-
求证：$DE\perp AG$；标注答案略解析如图，延长 $ED$ 交 $AG$ 于点 $H$．
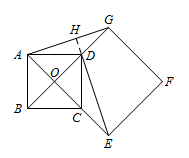因为 $ O$ 为正方形 $ABCD$ 两对角线的交点，
所以 $ OA=OD$，$OA\perp OD$．
因为 $ OG=OE$，
所以 $ \mathrm {Rt}\triangle AOG\cong \mathrm {Rt}\triangle DOE$，
所以 $ \angle AGO=\angle DEO$．
因为 $\angle AGO+\angle GAO=90^\circ $，
所以 $ \angle AGO+\angle DEO =90^\circ $，
所以 $\angle AHE=90^\circ $，
即 $DE\perp AG$． -
正方形 $ABCD$ 固定，将正方形 $OEFG$ 绕点 $O$ 逆时针旋转 $\alpha$ 角（$0^\circ <\alpha<360^\circ $）得到正方形 $OE'F'G'$，如图2．
$(1)$ 在旋转过程中，当 $\angle OAG'$ 是直角时，求 $\alpha$ 的度数；
$(2)$ 若正方形 $ABCD$ 的边长为 $1$，在旋转过程中，求 $AF'$ 长的最大值和此时 $\alpha$ 的度数，直接写出结果不必说明理由．标注答案$(1)$ $\alpha=30^\circ $ 或 $150^\circ $；
$(2)$ 即 $\alpha=315^\circ$ 时，$AF'$ 取最大值 $2+\dfrac{\sqrt 2}{2}$解析在旋转过程中，$\angle OAG'$ 成为直角有两种情况：
$(1)$ $\alpha$ 由 $0^\circ $ 增大到 $90^\circ $ 过程中，当 $\angle OAG'=90^\circ $ 时，
因为 $ OA=OD=\dfrac 12OG=\dfrac 12OG'$，
所以在 $\mathrm {Rt}\triangle OAG'$ 中，$\sin \angle AG'O=\dfrac{OA}{OG'}=\dfrac 12$，
所以 $\angle AG'O=30^\circ $，
因为 $OA\perp OD$，$OA\perp AG'$，
所以 $ OD\parallel AG'$，
所以 $\angle DOG'=\angle AG'O=30^\circ $，
即 $\alpha=30^\circ $；
② $\alpha$ 由 $90^\circ $ 增大到 $180^\circ $ 过程中，当 $\angle OAG'$ 为直角时，
同理可求 $\angle BOG'=30^\circ $，
所以 $\alpha=180^\circ -30^\circ =150^\circ $．
综上，当 $\angle OAG'$ 为直角时，$\alpha=30^\circ $ 或 $150^\circ $．
$(2)$ $AF'$ 长的最大值是 $2+\dfrac{\sqrt 2}{2}$，此时 $\alpha=315^\circ $．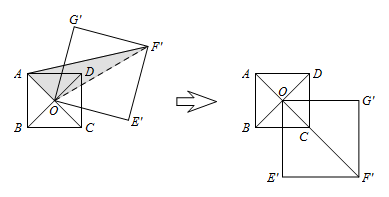
如图，$AF'\leqslant OA+OF'=2+\dfrac{\sqrt 2}{2}$，
所以当点 $O$ 在 $AF'$ 上，即 $\alpha=315^\circ$ 时，$AF'$ 取最大值 $2+\dfrac{\sqrt 2}{2}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
