边长为 $6$ 的等边 $\triangle ABC$ 中,点 $D,E$ 分别在 $AC,BC$ 边上,$DE\parallel AB$,$EC=2\sqrt 3$,将 $\triangle DEC$ 绕点 $C$ 旋转 $\alpha$($0^\circ<\alpha <360^\circ$),得到 $\triangle D'E'C$,连接 $AD',BE'$,边 $D'E'$ 的中点为 $P$,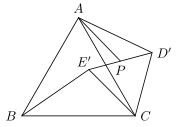

【难度】
【出处】
无
【标注】
-
在旋转过程中,$AD'$ 和 $BE'$ 有怎样的数量关系?并说明理由;标注答案$AD'=BE'$解析当 $\alpha \ne 180^\circ$ 时,由旋转的性质可得 $\angle ACD'=\angle BCE'$,
因为 $AC=BC,CD'=CE'$,
所以 $\triangle AC'D\cong \triangle BCE'$,
所以 $AD'=BE'$,
当 $\alpha=180^\circ$ 时,$AD'=AC+CD'$,$BE'=BC+CE'$,即 $AD'=BE'$. -
连接 $AP$,当 $AP$ 最大时,求 $AD'$ 的值.标注答案$AD'=2\sqrt{21}$解析连接 $CP$,在 $\triangle ACP$ 中,有三角形三边关系得 $AP<AC+CP$,
所以当 $A,C,P$ 三点共线时 $AP$ 最大. 此时 $AP=AC+CP$,
此时 $AP=AC+CP$,
在 $\triangle D'CE'$ 中,由 $P$ 为 $D'E'$ 中点,得 $AP\perp D'E',PD'=\sqrt 3$,
所以 $CP=3$,所以AP= $9$,
所以 $AD'=2\sqrt{21}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2