已知在 $\rm{Rt}\triangle BAC$ 中，$\angle BAC=90^\circ$，$AB=AC$，点 $D$ 为射线 $BC$ 上一点（与点 $B$ 不重合），过点 $C$ 作 $CE\perp BC$ 于点 $C$，且 $CE=BD$（点 $E$ 与点 $A$ 在射线 $BC$ 同侧），连接 $AD,ED$．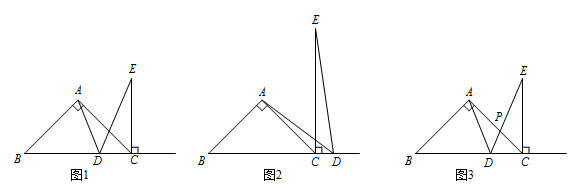
【难度】
【出处】
无
【标注】
-
如图1，当点 $D$ 在线段 $BC$ 上时，直接写出 $\angle ADE$ 的度数；标注答案$\angle ADE=45^\circ$解析略
-
当点 $D$ 在线段 $BC$ 的延长线上时，$(1)$ 中结论是否成立？若成立，请证明，若不成立，请说明理由；标注答案成立解析连接 $AE$．
在 $\rm{Rt}\triangle BAC$ 中，$\angle BAC=90^\circ$，$AB=AC$，
所以 $\angle B=\angle ACB=\angle ACE=45^\circ$，
因为 $CE=BD,AB=AC$，
所以 $\triangle ABC\cong \triangle ACE$，
所以 $\angle BAD=\angle CAE$，
所以 $\angle BAC=\angle DAE=90^\circ$，
因为 $AD=AE$，
所以 $\angle ADE=45^\circ$． -
在 $(1)$ 的条件下，$ED$ 与 $AC$ 相交于点 $P$，若 $AB=2$，求出 $CP$ 的最大值．标注答案$CP$ 最大值为 $1$解析因为 $AC$ 的长度固定，若 $PC$ 有最大值，$AP$ 有最小值，
因为点 $A$ 到 $DE$ 距离最短，
所以当 $AP\perp DE$ 时，$AP$ 最小，$PC$ 最大．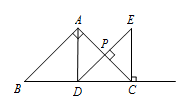
所以 $PC$ 最大值为 $1$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
