如图，在 $\triangle ABC$ 中，$\angle B=90^\circ$，$AB=CB=2$，以点 $B$ 为圆心作 $\odot B$ 与 $AC$ 相切，点 $P$ 为 $\odot B$ 上任意一点，求 $PA+\dfrac{\sqrt 2}2PC$ 的最小值．
【难度】
【出处】
无
【标注】
【答案】
$PA+\dfrac{\sqrt 2}2PC$ 的最小值为 $\sqrt 5$
【解析】
如图，过点 $B$ 作 $BD\perp AC$ 于点 $D$，则 $BD=\sqrt 2$．
连接 $PB$，则 $BP=\dfrac{\sqrt 2}{2}BC$．
取 $BC$ 的中点 $E$，则 $BE=\dfrac{\sqrt 2}{2}BP$．
连接 $PE$，易证 $\triangle PBE\backsim \triangle CBP$，所以 $PE=\dfrac{\sqrt 2}{2}PC$．
连接 $AE$，则 $AE=\sqrt{AB^2+EB^2}=\sqrt 5$．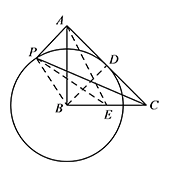
所以 $PA+\dfrac{\sqrt 2}2PC$ 的最小值为 $\sqrt 5$．
连接 $PB$，则 $BP=\dfrac{\sqrt 2}{2}BC$．
取 $BC$ 的中点 $E$，则 $BE=\dfrac{\sqrt 2}{2}BP$．
连接 $PE$，易证 $\triangle PBE\backsim \triangle CBP$，所以 $PE=\dfrac{\sqrt 2}{2}PC$．
连接 $AE$，则 $AE=\sqrt{AB^2+EB^2}=\sqrt 5$．
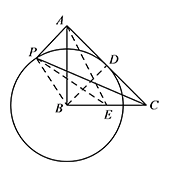所以 $PA+\dfrac{\sqrt 2}2PC$ 的最小值为 $\sqrt 5$．
答案
解析
备注
