如图，在平面直角坐标系 $xOy$ 中，$A\left(-6,0\right),B\left(6,0\right),C\left(0,4\sqrt 3\right)$，设 $G$ 为 $y$ 轴上一点，点 $P$ 从直线 $y=-\sqrt 3x+6\sqrt 3$ 与 $y$ 轴的交点 $M$ 出发，先沿 $y$ 轴到达 $G$ 点，再沿 $GA$ 到达 $A$ 点，若 $P$ 点在 $y$ 轴上运动的速度是它在直线 $GA$ 上运动速度的 $2$ 倍，试确定 $G$ 点的位置，使点 $P$ 按照上述要求到达 $A$ 点所用的时间最短．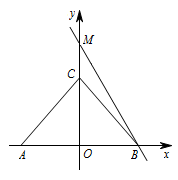
【难度】
【出处】
无
【标注】
【答案】
$G$ 点的坐标为 $\left(0,2\sqrt 3\right)$
【解析】
设点 $P$ 在 $GM$ 上的运动速度为 $2v$，点 $P$ 在 $GA$ 上的运动速度为 $v$，
所以 $t=\dfrac{GM}{2v}+\dfrac{GA}{v}=\dfrac 1v\left(\dfrac 12GM+GA\right)$，
所以当 $\dfrac 12GM+GA$ 取最小值，时间最短．
易得 $M\left(0,6\sqrt3\right)$，所以 $OM=6\sqrt 3$．
由 $OB=6$，可得 $BM=12$．
所以 $\sin\angle BMO=\dfrac 12$．
过点 $A$ 作 $AH\perp BM$ 于点 $H$，则 $AH$ 与 $y$ 轴的交点为所求的 $G$ 点．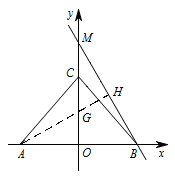
此时 $GH=\dfrac 12GM$，所以 $\dfrac 12GM+GA$ 最小值即为 $AH$ 的长．
在 $\mathrm {Rt}\triangle OAG$ 中，$OG=AO\cdot \tan \angle BAH=2\sqrt 3$，
所以 $G$ 点的坐标为 $\left(0,2\sqrt 3\right)$．
所以 $t=\dfrac{GM}{2v}+\dfrac{GA}{v}=\dfrac 1v\left(\dfrac 12GM+GA\right)$，
所以当 $\dfrac 12GM+GA$ 取最小值，时间最短．
易得 $M\left(0,6\sqrt3\right)$，所以 $OM=6\sqrt 3$．
由 $OB=6$，可得 $BM=12$．
所以 $\sin\angle BMO=\dfrac 12$．
过点 $A$ 作 $AH\perp BM$ 于点 $H$，则 $AH$ 与 $y$ 轴的交点为所求的 $G$ 点．
此时 $GH=\dfrac 12GM$，所以 $\dfrac 12GM+GA$ 最小值即为 $AH$ 的长．在 $\mathrm {Rt}\triangle OAG$ 中，$OG=AO\cdot \tan \angle BAH=2\sqrt 3$，
所以 $G$ 点的坐标为 $\left(0,2\sqrt 3\right)$．
答案
解析
备注
