如图，点 $E$ 是过 $A(-4,-4),B(0,4)$ 两点的直线上的动点，直线 $AC:y=-\dfrac 12x-6$ 交 $y$ 轴于点 $C$，过点 $E$ 作 $EF\perp x$ 轴交 $AC$ 于点 $F$．
【难度】
【出处】
无
【标注】
-
在 $y$ 轴上存在着一点 $D$，连接 $ED,DF$，当点 $E$ 运动到什么位置时，以 $A,E,F,D$ 为顶点的四边形是矩形？求出此时点 $E,D$ 的坐标；标注答案点 $E$ 的坐标为 $(-2,0)$，点 $D$ 的坐标为 $(0,-1)$解析由题意可得直线 $AB$ 的解析式为 $y=2x+4$，点 $C$ 的坐标为 $(0,-6)$．
所以 $AB^2=(-4)^2+(-4-4)^2=80$，
$AC^2=(-4)^2+(-4+6)^2=20$，$BC^=100$，
从而有 $AB^2+AC^2=BC^2$，即 $\angle BAC=90^\circ$．
欲使以 $A,E,F,D$ 为顶点的四边形是矩形，
只需四边形 $AEDF$ 为平行四边形即可．
可设点 $E(m,2m+4)$，点 $D(0,n)$，则点 $F\left(m,-\dfrac 12m-6\right)$．由平行四边形对角线互相平分可得 $\begin{cases}-4+0=m+m,\\-4+n=2m+4-\dfrac 12m-6.\end{cases}$
解得 $\begin{cases}m=-2,\\n=-1.\end{cases}$
所以点 $E$ 的坐标为 $(-2,0)$，点 $D$ 的坐标为 $(0,-1)$． -
在第1问的前提下，以点 $E$ 为圆心，$ED$ 长为半径作圆，点 $M$ 为 $\odot E$ 上一动点，求 $\dfrac 12AM+CM$ 的最小值．标注答案$\dfrac 12AM+CM$ 的最小值为 $\dfrac{5\sqrt 5}2$解析易求 $AE=2\sqrt 5$，$DE=\sqrt 5$，
如图，连接 $ME$，则 $ME=DE=\dfrac 12 AE$．
在 $AE$ 上取一点 $G$，使得 $GE=\dfrac 12ME$．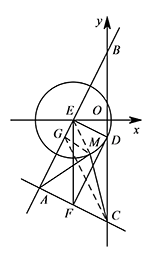
连接 $MG$，则 $\triangle MEG\backsim \triangle AEM$，
所以 $MG=\dfrac 12MA$，
连接 $CG$，则 $CG$ 的长即为 $\dfrac 12AM+CM$ 的最小值．
而 $AG=\dfrac{3\sqrt 5}2$，$AC=2\sqrt 5$，
所以在 $\mathrm{RT}\triangle CAG$ 中，可得 $CG=\sqrt{AG^2+AC^2}=\dfrac{5\sqrt 5}2$，
即 $\dfrac 12AM+CM$ 的最小值为 $\dfrac{5\sqrt 5}2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
