如图1，抛物线 $y=ax^2+(a+3)x+3(a\ne0)$ 与 $x$ 轴交于点 $A(4,0)$，与 $y$ 轴交于点 $B$，在 $x$ 轴上有一动点 $E(m,0)(0<m<4)$，过点 $E$ 作 $x$ 轴的垂线交直线 $AB$ 于点 $N$，交抛物线于点 $P$，过点 $P$ 作 $PM\perp AB$ 于点 $M$．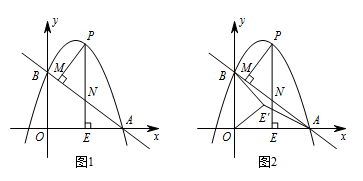
【难度】
【出处】
无
【标注】
-
设 $\triangle PMN$ 的周长为 $C_1$，$\triangle AEN$ 的周长为 $C_2$，若 $\dfrac{C_1}{C_2}=\dfrac 65$，求 $m$ 的値；标注答案$m$ 的値为 $2$解析把点 $A(4,0)$ 的坐标代入 $y=ax^2+(a+3)x+3$，
得 $16a+4(a+3)+3=0$，解得 $a=-\dfrac34$．
所以抛物线的函数表达式为 $y=-\dfrac 34x^2+\dfrac94x+3$．
当 $x=0$ 时，$y=3$，所以点 $B$ 的坐标为 $(0,3)$，
从而 $AB=\sqrt{OA^2+OB^2}=5$．
根据题意，得 $OE=m$，$AE=4-m$，
所以点 $P$ 的坐标为 $\left(m,-\dfrac 34m^2+\dfrac94m+3\right)$．
所以 $PE=-\dfrac 34m^2+\dfrac 94m+3$
因为 $\triangle AEN\backsim \triangle AOB$，
所以 $\dfrac{AN}{AB}=\dfrac{NE}{BO}=\dfrac {AE}{AO}$，即 $\dfrac {AN}{5}=\dfrac{NE}{3}=\dfrac {4-m}{4}$．
所以 $AN=\dfrac 54(4-m)$，$ NE=\dfrac 34(4-m)$．
因为 $\triangle PMN\backsim \triangle AEN$，且 $\dfrac{C_1}{C_2} =\dfrac 65$，
所以 $\dfrac {PN}{AN}=\dfrac 65$．
所以 $PN=\dfrac 65 AN=\dfrac 65 \times\dfrac 54(4-m)=\dfrac 32(4-m)$．
而 $PE=NE+PN$，
所以 $\dfrac 34(4-m)+\dfrac 32(4-m)=\dfrac 94(4-m)$，
解得 $m_1=2$，$m_2=4$（不合题意，舍去）．
所以此时 $m$ 的値为 $2$． -
如图2，在第1问的条件下，将线段 $OE$ 绕点 $O$ 逆时针旋转得到 $OE'$，旋转角为 $\alpha (0^\circ< \alpha <90^\circ)$，连接 $E'A$、$E'B$，求 $E'A+\dfrac 23E'B$ 的最小值．标注答案$E'A+\dfrac 23E'B$ 的最小值为 $\dfrac 43\sqrt{10}$解析在第1问的条件下 $m=2$，所以点 $E(2,0)$，
从而 $OE'=OE=2=\dfrac 23OB$．
如图，在 $OB$ 上取点 $F$，使得 $OF=\dfrac 23OE'$，连接 $FE'$．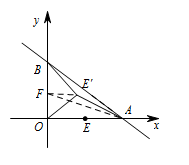
易证 $\triangle E'OF\backsim \triangle BOE'$，
所以 $E'F=\dfrac 23E'B$．
连接 $AF$，从而 $E'A+\dfrac 23E'B=E'A+E'F\geqslant AF$．
而 $AF=\sqrt{4^2+\left(\dfrac 43\right)^2}=\dfrac43\sqrt{10}$，
所以 $E'A+\dfrac 23E'B$ 的最小值为 $\dfrac 43\sqrt{10}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
