如图，抛物线 $y=ax^2+bx-a-b$（$a<0$，$a,b$ 为常数）与 $x$ 轴交于 $A,C$ 两点，与 $y$ 轴交于 $B$ 点．直线 $AB$ 的函数关系式为 $y=\dfrac 89x+\dfrac{16}3$．已知点 $M$ 是线段 $OA$ 上的一个动点，过点 $M$ 作 $x$ 轴的垂线 $l$ 分别与直线 $AB$ 和抛物线交于 $D,E$ 两点．若 $\triangle BDE$ 是以 $DE$ 为底边的等腰三角形，将 $OM$ 绕原点 $O$ 顺时针旋转得到 $ON$（旋转角在 $0^\circ$ 到 $90^\circ$ 之间）．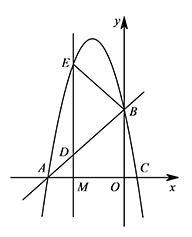
【难度】
【出处】
无
【标注】
-
求点 $M$ 的坐标；标注答案点 $M$ 的坐标为 $(-4,0)$解析由直线 $AB$ 的函数关系式可得点 $A(-6,0)$，点 $B\left(0,\dfrac{16}3\right)$．
将其代入抛物线解析式得 $\begin{cases}36a-6b-a-b=0,\\-a-b=\dfrac{16}3,\end{cases}$
解得 $\begin{cases}a=-\dfrac 89,\\b=-\dfrac{40}9.\end{cases}$
所以抛物线解析式为 $y=-\dfrac 89x^2-\dfrac{40}9x+\dfrac{16}3$．
设点 $M$ 的坐标为 $(-m,0)$，则点 $E$ 的坐标为 $\left(-m,-\dfrac 89m^2+\dfrac{40}9m+\dfrac{16}3\right)$．
过点 $B$ 作 $BF\perp DE$ 于点 $F$，则 $\angle EBF=\angle DBF=\angle BAO$．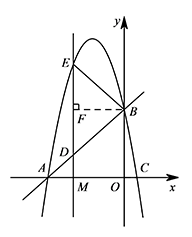
所以 $\tan\angle EBF=\angle BAC$，即 $\dfrac{EF}{BF}=\dfrac{BC}{AC}$，
所以 $\dfrac{-\dfrac 89m^2+\dfrac{40}9m+\dfrac{16}3-\dfrac{16}3}{m}=\dfrac{\dfrac{16}3}{6}$，
化简得 $m(m-4)=0$，解得 $m_1=4$，$m_2=0$（舍去）．
所以点 $M$ 的坐标为 $(-4,0)$． -
线段 $OB$ 上是否存在定点 $P$（不与 $O,B$ 重合），无论 $ON$ 如何旋转，$\dfrac{NP}{NB}$ 始终保持不变．若存在，试求出 $P$ 点坐标；若不存在，请说明理由；标注答案存在，点 $P$ 的坐标为 $(0,3)$解析由题意可得点 $N$ 在以 $O$ 为圆心、$OM$ 为半径且在第二象限内的圆弧上．
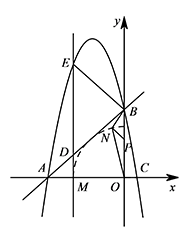在 $OB$ 上取点 $P$，使得 $\dfrac{OP}{ON}=\dfrac{ON}{OB}$．
此时 $\triangle PON\backsim \triangle NOB$，
所以 $\dfrac{NP}{NB}=\dfrac{ON}{OB}=\dfrac 34$，即 $\dfrac{NP}{NB}$ 为定值．
而 $\dfrac{OP}{4}=\dfrac{4}{\dfrac{16}{3}}$，即 $OP=3$，
所以此时点 $P$ 的坐标为 $(0,3)$． -
试求出此旋转过程中，$NA+\dfrac 34 NB$ 的最小值．标注答案$NA+\dfrac 34NB$ 的最小值为 $3\sqrt 5$解析由第2问可得 $NP=\dfrac 34 NB$，
所以 $NA+\dfrac 34NB=NA+NP\geqslant AP$．
如图，当点 $N$ 在 $AP$ 上，$NA+\dfrac 34NB$ 最小，最小值即为 $AP$ 的长．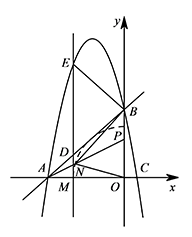
而 $AP=\sqrt{OA^2+OP^2}=\sqrt{36+9}=3\sqrt 5$，
所以 $NA+\dfrac 34NB$ 的最小值为 $3\sqrt 5$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
