如图，在平面直角坐标系 $xOy$ 中，$A\left(-6,0\right)$，$B\left(6,0\right)$，$C\left(0,4\sqrt 3\right)$，延长 $AC$ 到点 $D$，使 $CD=\dfrac 12AC$，过点 $D$ 作 $DE\parallel AB$ 交 $BC$ 的延长线于点 $E$．设 $G$ 为 $y$ 轴上一点，点 $P$ 从直线 $y=-\sqrt 3x+6\sqrt 3$ 与 $y$ 轴的交点 $M$ 出发，先沿 $y$ 轴到达 $G$ 点，再沿 $GA$ 到达 $A$ 点，若 $P$ 点在 $y$ 轴上运动的速度是它在直线 $GA$ 上运动速度的 $2$ 倍，试确定 $G$ 点的位置，使点 $P$ 按照上述要求到达 $A$ 点所用的时间最短．
【难度】
【出处】
无
【标注】
【答案】
所以 $G$ 点的坐标为 $\left(0,2\sqrt 3\right)$
【解析】
因为 $t=\dfrac{GM}{2v}+\dfrac{GA}{v}=\dfrac {2GA+GM}{2v}$，
所以当 $2GA+GM$ 最小时，时间最短．
如图，假设在 $OM$ 一点 $G$，则 $BG=AG$，
所以 $MG+2AG=MG+AG+BG$．
把 $\triangle MGB$ 绕点 $B$ 顺时针旋转 $60^\circ$，得到 $\triangle M'G'B$，连接 $GG',MM'$，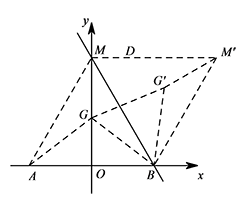
所以 $\triangle GG'B,\triangle MM'B$ 都是等边三角形，
则 $GG'=BG'=BG$．
又因为 $M'G'=MG$，
所以 $MG+AG+BG=M'G'+GG'+AG$．
因为点 $A,M'$ 为定点，所以 $AM'$ 与 $OM$ 的交点为 $G$，此时 $MG+AG+BG$ 最小．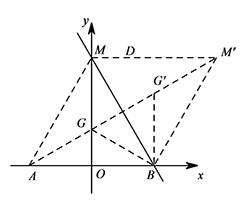
所以 $G$ 点的坐标为 $\left(0,2\sqrt 3\right)$．
所以当 $2GA+GM$ 最小时，时间最短．
如图，假设在 $OM$ 一点 $G$，则 $BG=AG$，
所以 $MG+2AG=MG+AG+BG$．
把 $\triangle MGB$ 绕点 $B$ 顺时针旋转 $60^\circ$，得到 $\triangle M'G'B$，连接 $GG',MM'$，
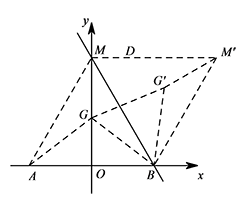所以 $\triangle GG'B,\triangle MM'B$ 都是等边三角形，则 $GG'=BG'=BG$．
又因为 $M'G'=MG$，
所以 $MG+AG+BG=M'G'+GG'+AG$．
因为点 $A,M'$ 为定点，所以 $AM'$ 与 $OM$ 的交点为 $G$，此时 $MG+AG+BG$ 最小．
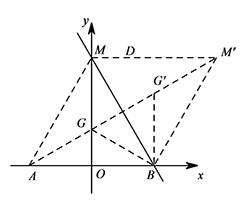所以 $G$ 点的坐标为 $\left(0,2\sqrt 3\right)$．
答案
解析
备注
