$A,B,C,D$ 四个城市恰好为一个正方形的四个顶点,要建立一个公路系统,使每两个城市之间都有公路相通,并使整个公路系统的总长为最小,则这个公路系统应当如何修建?

【难度】
【出处】
无
【标注】
【答案】
当点 $E$、点 $M$、点 $P$、点 $Q$、点 $N$、点 $F$ 共线时,整个公路系统的总长最小值为 $EF$ 的长.此时 $P,Q$ 在 $EF$ 上,如图所示.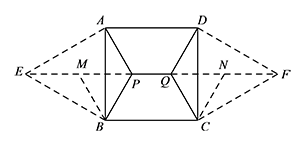
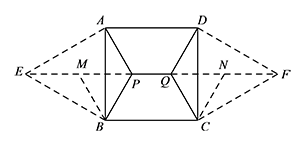
【解析】
如图所示,将 $\triangle ABP$ 绕点 $B$ 逆时针旋转 $60^\circ$,得到 $\triangle EBM$;同样将 $\triangle DCQ$ 绕点 $C$ 顺时针旋转 $60^\circ$,得到 $\triangle FCN$.连接 $AE,DF$,则 $\triangle ABE,\triangle DCF$ 均为等边三角形,连接 $PM,QN$,则 $\triangle BPM,\triangle CQN$ 均为等边三角形. 所以当点 $E$、点 $M$、点 $P$、点 $Q$、点 $N$、点 $F$ 共线时,整个公路系统的总长最小值为 $EF$ 的长.此时 $P,Q$ 在 $EF$ 上,如图所示.
所以当点 $E$、点 $M$、点 $P$、点 $Q$、点 $N$、点 $F$ 共线时,整个公路系统的总长最小值为 $EF$ 的长.此时 $P,Q$ 在 $EF$ 上,如图所示.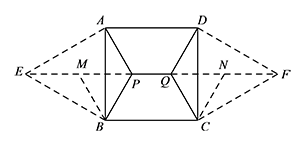
 所以当点 $E$、点 $M$、点 $P$、点 $Q$、点 $N$、点 $F$ 共线时,整个公路系统的总长最小值为 $EF$ 的长.此时 $P,Q$ 在 $EF$ 上,如图所示.
所以当点 $E$、点 $M$、点 $P$、点 $Q$、点 $N$、点 $F$ 共线时,整个公路系统的总长最小值为 $EF$ 的长.此时 $P,Q$ 在 $EF$ 上,如图所示.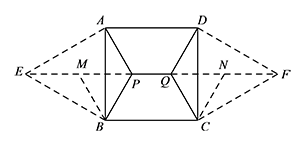
答案
解析
备注