已知 $\triangle ABC$ 中，$\angle ABC=60^\circ$，$AB=5$，$BC=3$，$P$ 是 $\triangle ABC$ 内一点，求 $PA+PB+PC$ 的最小值，并确定当 $PA+PB+PC$ 取得最小值时 $\angle APC$ 的度数．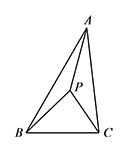
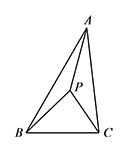
【难度】
【出处】
无
【标注】
【答案】
$\angle APC=120^\circ$
【解析】
如图，将 $\triangle APB$ 绕点 $B$ 逆时针旋转 $60^\circ$，得到 $\triangle A'BP'$．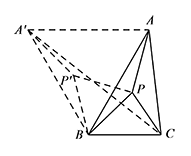
连接 $PP',A'C,AA'$，则 $\triangle BPP',\triangle BAA'$ 均为等边三角形，
所以 $PA+PB+PC=A'P'+P'P+PC\geqslant A'C$．
故当 $A',P',P,C$ 四点共线时，$PA+PB+PC$ 取最小值，最小值即为 $A'C$ 的长．
此时 $\angle APB=\angle A'P'B=120^\circ=\angle BPC$，
所以 $\angle APC=120^\circ$．
过点 $A'$ 作 $A'E\perp BC$ 的延长线于点 $E$，则 $\angle A'BE=60^\circ$．
所以 $BE=\dfrac 12 A'B=\dfrac 52$，$A'E=\dfrac{\sqrt 3}{2}A'B=\dfrac{5\sqrt 3}2$，
所以 $EC=BE+BC=\dfrac {11}2$，
从而 $A'C=\sqrt{{A'E}^2+{EC}^2}=7$．
综上可得，$PA+PB+PC$ 的最小值为 $7$，且此时 $\angle APC=120^\circ$．
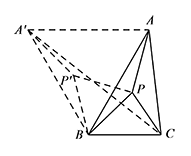连接 $PP',A'C,AA'$，则 $\triangle BPP',\triangle BAA'$ 均为等边三角形，所以 $PA+PB+PC=A'P'+P'P+PC\geqslant A'C$．
故当 $A',P',P,C$ 四点共线时，$PA+PB+PC$ 取最小值，最小值即为 $A'C$ 的长．
此时 $\angle APB=\angle A'P'B=120^\circ=\angle BPC$，
所以 $\angle APC=120^\circ$．
过点 $A'$ 作 $A'E\perp BC$ 的延长线于点 $E$，则 $\angle A'BE=60^\circ$．所以 $BE=\dfrac 12 A'B=\dfrac 52$，$A'E=\dfrac{\sqrt 3}{2}A'B=\dfrac{5\sqrt 3}2$，
所以 $EC=BE+BC=\dfrac {11}2$，
从而 $A'C=\sqrt{{A'E}^2+{EC}^2}=7$．
综上可得，$PA+PB+PC$ 的最小值为 $7$，且此时 $\angle APC=120^\circ$．
答案
解析
备注
