在 $\triangle ABC$ 中，$\angle ACB=90^\circ$，$AC>BC$，$D$ 是 $AC$ 边上的动点，$E$ 是 $BC$ 边上的点，$AD=BC$，$CD=BE$．点 $E$ 与点 $B,C$ 不重合，连接 $AE,BD$ 交于点 $F$，求出 $\angle BFE$ 的度数．
【难度】
【出处】
无
【标注】
【答案】
$\angle BFE=\angle GBD=45^\circ$
【解析】
如图，过点 $A$ 作 $AG\perp AC$，使得 $AG=CD=BE$，连接 $BG,GD$．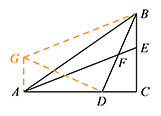
可得四边形 $AEBG$ 是平行四边形，则 $BG\parallel EA$．
易证 $\triangle GAD\cong \triangle DCB (\mathrm {SAS})$，
所以 $GD=DB$，$\angle GDA=\angle DBC$．
所以 $\angle GDA+\angle BDC=90^\circ$，
可得 $\triangle BGD$ 是等腰直角三角形．
又因为 $BG\parallel EF$，
所以 $\angle BFE=\angle GBD=45^\circ$．
可得四边形 $AEBG$ 是平行四边形，则 $BG\parallel EA$．易证 $\triangle GAD\cong \triangle DCB (\mathrm {SAS})$，
所以 $GD=DB$，$\angle GDA=\angle DBC$．
所以 $\angle GDA+\angle BDC=90^\circ$，
可得 $\triangle BGD$ 是等腰直角三角形．
又因为 $BG\parallel EF$，
所以 $\angle BFE=\angle GBD=45^\circ$．
答案
解析
备注
