如图所示，两条长度为 $1$ 的线段 $AB$ 和 $CD$ 相交于 $O$ 点，且 $\angle AOC=60^\circ$，求证：$AC+BD\geqslant 1$．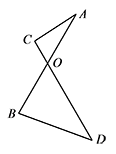
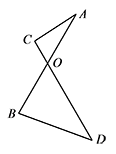
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
分别过点 $C,B$ 作 $AB,AC$ 的平行线，两线交于点 $E$，连接 $DE$．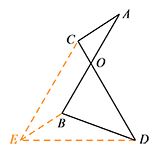
则四边形 $ABEC$ 是平行四边形，$\triangle CDE$ 是等边三角形，
从而 $AC=BE$，$DE=DC=1$．
所以 $AC+BD=BE+BD\geqslant DE$，
即 $AC+BD\geqslant1$．
则四边形 $ABEC$ 是平行四边形，$\triangle CDE$ 是等边三角形，从而 $AC=BE$，$DE=DC=1$．
所以 $AC+BD=BE+BD\geqslant DE$，
即 $AC+BD\geqslant1$．
答案
解析
备注
