在 $\mathrm {Rt}\triangle ABC$ 中，$\angle C=90^\circ$，$D,E$ 分别为 $CB,CA$ 延长线上的点，$BE,AD$ 交于点 $P$．若 $AC=\sqrt3BD$，$CD=\sqrt3AE$，求 $\angle APE$ 的度数．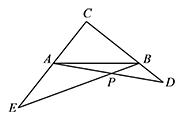
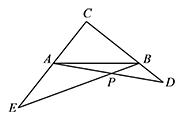
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
过点 $D$ 作 $DF\parallel BE$，使得 $DF=BE$，连接 $EF,AF$．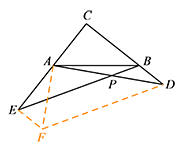
则四边形 $EFDB$ 为平行四边形，
所以 $AC=\sqrt3BD=\sqrt3EF$．
所以 $\dfrac{AC}{EF}=\dfrac{CD}{AE}=\sqrt3$．
而 $\angle AEF=\angle C=90^\circ$，
则 $\triangle AEF\backsim\triangle DCA$．
所以 $\dfrac{AD}{AF}=\sqrt3$，$\angle EAF=\angle CDA$．
所以 $\angle EAF+\angle CAD=90^\circ$，$\angle FAD=90^\circ$．
故 $\angle APE=\angle ADF=30^\circ$．
则四边形 $EFDB$ 为平行四边形，所以 $AC=\sqrt3BD=\sqrt3EF$．
所以 $\dfrac{AC}{EF}=\dfrac{CD}{AE}=\sqrt3$．
而 $\angle AEF=\angle C=90^\circ$，
则 $\triangle AEF\backsim\triangle DCA$．
所以 $\dfrac{AD}{AF}=\sqrt3$，$\angle EAF=\angle CDA$．
所以 $\angle EAF+\angle CAD=90^\circ$，$\angle FAD=90^\circ$．
故 $\angle APE=\angle ADF=30^\circ$．
答案
解析
备注
