已知函数 $y=\ln x-(ax+b)$ 有两个不同的零点 $x_1,x_2$，求证：$\dfrac{{\mathrm e}^{1+b}}{a}<x_1x_2<\dfrac{1}{a^2}$．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
问题等价于 $f_1(x)=x-a{\mathrm e}^x-b$ 有两个不同的零点 $x_1,x_2$，求证：$$1+b-\ln a<x_1+x_2<-2\ln a.$$尝试使用构造函数的方法证明极值点偏移不等式．
右边不等式 由于 $f_1'(x)=1-a{\mathrm e}^x$，因此 $a>0$，其极值点为 $x=-\ln a$．又由于函数 $f_1(x)$ 的二阶导函数 $f_1''(x)=-a{\mathrm e}^x$，因此构造函数$$g_1(x)=\dfrac 12f_{1}''(-\ln a)\cdot(x+\ln a)^2+f_{1}(-\ln a),$$则 $h_1(x)=f_1(x)-g_1(x)$ 的二阶导函数$$h_1''(x)=f_{1}''(x)-f_{1}''(-\ln a)=1-a{\mathrm e}^x,$$因此在 $(-\infty,-\ln a)$ 上，$h_1''(x)>0$，在 $(-\ln a,+\infty)$ 上，$h_1''(x)<0$；结合 $h_1'(-\ln a)=0$，在 $\mathbb R$ 上，$h_1'(x)\leqslant 0$；结合 $h_1(-\ln a)=0$，在 $(-\infty,-\ln a)$ 上，$h_1(x)>0$，在 $(-\ln a,+\infty)$ 上，$h_1(x)<0$，如图．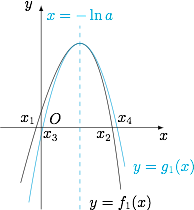
因此二次函数 $g_1(x)=\dfrac 12f_{1}''(-\ln a)\cdot(x+\ln a)^2+f_{1}(-\ln a)$ 的零点 $x_3,x_4$（$x_3<x_4$）满足$$x_1<x_3<x_2<x_4,$$因此 $x_1+x_2<x_3+x_4=-2\ln a$．
左边不等式 此时无法通过构造二次函数证明．设 $f_2(x)=\ln x-(ax+b)$，则其导函数 $f_2'(x)=\dfrac 1x-a$，因此其极大值点为 $x=\dfrac 1a$．欲证明的不等式为$$\ln x_1+\ln x_2>1+b-\ln a,$$即$$x_1+x_2>\dfrac{1-b-\ln a}a.$$构造函数$$g_2(x)=\dfrac 1{\alpha x+\beta}+\gamma -(ax+b),$$其中 $g_2(x)$ 与 $f_2(x)$ 在 $x=\dfrac 1a$ 处的函数值，导函数值和二阶导函数值均相等，则可以求得$$g_2(x)=-\dfrac{4}{ax+1}+2-\ln a-(ax+b),$$此时 $h_2(x)=f_2(x)-g_2(x)$ 的导函数$$h_2'(x)=\dfrac 1x-\dfrac{4a}{(ax+1)^2}=\dfrac{(ax-1)^2}{x(ax+1)^2}\geqslant 0,$$结合 $h_2\left(\dfrac 1a\right)=0$ 可得 $h_2(x)$ 在 $x=\dfrac 1a$ 的两侧异号，如图．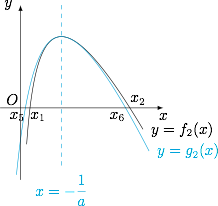
而函数 $g_2(x)$ 的零点 $x_5,x_6$（$x_5<x_6$）即方程$$\dfrac{-a^2x^2+a(1-\ln a-b)-4}{ax+1}=0$$的两根，有 $x_5+x_6=\dfrac{1-b-\ln a}a$，因此$$x_5<x_1<x_6<x_2,$$可得 $x_1+x_2>x_5+x_6>\dfrac{1-b-\ln a}a$，原命题得证．
因此二次函数 $g_1(x)=\dfrac 12f_{1}''(-\ln a)\cdot(x+\ln a)^2+f_{1}(-\ln a)$ 的零点 $x_3,x_4$（$x_3<x_4$）满足$$x_1<x_3<x_2<x_4,$$因此 $x_1+x_2<x_3+x_4=-2\ln a$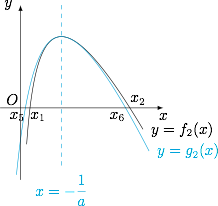．而函数 $g_2(x)$ 的零点 $x_5,x_6$（$x_5<x_6$）即方程$$\dfrac{-a^2x^2+a(1-\ln a-b)-4}{ax+1}=0$$的两根，有 $x_5+x_6=\dfrac{1-b-\ln a}a$，因此$$x_5<x_1<x_6<x_2,$$可得 $x_1+x_2>x_5+x_6>\dfrac{1-b-\ln a}a$，原命题得证．
答案
解析
备注
