无

• 题型

  >

  微积分初步

  >

  函数不等式的证明

略

分段寻找分界函数即可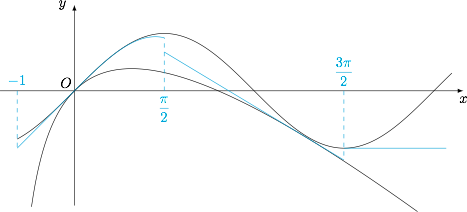．情形一 $-1<x\leqslant 0$，此时证明$$\sin x\geqslant x>2\ln (x+1)-x,$$这显然成立．
情形二 $0<x<\dfrac {\pi}2$，此时证明$$\sin x\geqslant x-\dfrac 16x^3>2\ln (x+1)-x.$$一方面，令$$f_1(x)=\sin x-\left(x-\dfrac 16x^3\right),$$则其导函数$$f_1'(x)=\cos x-1+\dfrac 12x^2=2\left(\dfrac x2\right)^2-2\sin^2\dfrac x2>0,$$于是左边不等式成立．
另一方面，令$$g_1(x)=2\ln(x+1)-x-\left(x-\dfrac 16x^3\right),$$则其导函数$$g_1'(x)=\dfrac{x(x^2+x-4)}{2(x+1)},$$于是当 $x\in\left(0,\dfrac {\pi}2\right)$ 时，$g_1(x)$ 先减后增，由 $g_1(0)=0,g_1\left(\dfrac {\pi}{2}\right )<0$ 知右边不等式成立．
情形三 $\dfrac {\pi}2\leqslant x\leqslant \dfrac{3\pi}2$，此时证明$$\sin x> -\dfrac 35(x-4)+2\ln 5-4\geqslant 2\ln(x+1)-x.$$一方面，令$$f_2(x)=\sin x-\left[-\dfrac 35(x-4)+2\ln 5-4\right],$$则其导函数$$f_2'(x)=\cos x+\dfrac 35,$$因此函数 $f_2(x)$ 在 $\left(\dfrac{\pi}2,\pi-\arccos\dfrac 35\right)$ 上单调递增，在 $\left(\pi-\arccos\dfrac 35,\pi+\arccos\dfrac 35\right)$ 上单调递减，在 $\left(\pi+\arccos\dfrac 35,\dfrac{3\pi}2\right)$ 上单调递增，因此该函数在区间 $\left[\dfrac{\pi}2,\dfrac{3\pi}2\right]$ 上的最小值为 $\min\left\{f_2\left(\dfrac{\pi}2\right),f_2\left(\pi+\arccos\dfrac 35\right)\right\}$．而$$f_2\left(\dfrac{\pi}2\right)=\dfrac{13}5+\dfrac{3\pi}{10}-2\ln5>0.3>0,$$且$$f_2\left(\pi+\arccos\dfrac 35\right)=\dfrac 45+\dfrac{3\pi}5+\dfrac 35\arccos\dfrac 35-2\ln 5>0,$$因此左边不等式成立．
另一方面，令$$g_2(x)=2\ln(x+1)-x-\left[-\dfrac 35(x-4)+2\ln 5-4\right],$$则其导函数$$g_2'(x)=\dfrac{2(4-x)}{5(x+1)},$$于是函数 $g_2(x)$ 在 $\left(\dfrac{\pi}2,4\right)$ 上单调递增，在 $\left(4,\dfrac{3\pi}2\right)$ 上单调递减，因此该函数在 $x=4$ 处取得极大值，亦为最大值 $g_2(4)=0$，因此右边不等式成立．
情形四 $x>\dfrac{3\pi}2$．此时证明$$\sin x\geqslant -1>2\ln(x+1)-x,$$这显然成立．
综合以上四种情形，我们就证明了 $\sin x + x\geqslant 2\ln (x+1)$．