菱形纸片 $ABCD$ 的边长为 $2$,折叠菱形纸片,将 $B,D$ 两点重合在对角线 $BD$ 上的同一点处,折痕分别为 $EF,GH$.当重合点在对角线 $BD$ 上移动时,探究六边形 $AEFCHG$ 的周长的变化情况.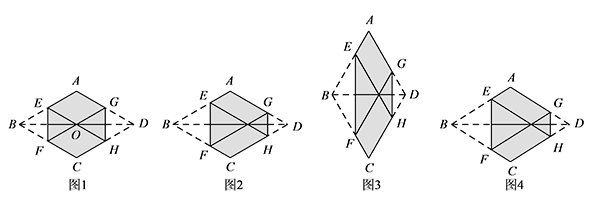

【难度】
【出处】
无
【标注】
-
若 $\angle ABC=60^\circ$,如图1,当重合点在菱形的对称中心 $O$ 处时,六边形 $AEFCHG$ 的周长为
$\triangle EBF,\triangle GHD$ 为等边三角形,
所以 $EF=BE$,$GH=GD$.
因为四边形 $FCDG,AEHD$ 为平行四边形.
所以 $FC=GD=DH=AE$.
同理 $CH=BE=AG$.
所以六边形 $AEFCHG$ 的周长恒为 $6$. -
如果菱形纸片 $ABCD$ 的边长仍为 $2$,改变 $\angle ABC$ 的大小,如图3,若 $\angle ABC=120^\circ$,则六边形 $AEFCHG$ 的周长为
因为 $AE=DH=DG=FC$,$AG=BF=BE=CH$.
所以 $C_{\text{六边形}AEFCHG}=AB+AD+\sqrt 3BE+\sqrt 3GD=4+2\sqrt 3$.
当 $\angle ABC=2\alpha$ 时,$EF=2BE\cdot \sin\alpha$,$GH=2DG\cdot \sin\alpha$.
所以 $C_{\text{六边形}AEFCHG}=AB+AD+2\sin\alpha \left(BE+DG\right)=AB+AD+2\sin\alpha\cdot AB=4+4\sin\alpha$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2