如图,已知 $\angle ABD=\angle ACD=60^\circ$,且 $\angle ADB=90^\circ-\dfrac 12\angle BDC$,求证:$\triangle ABC$ 是等腰三角形.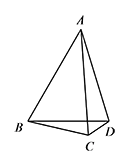
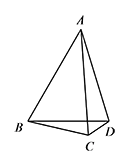
【难度】
【出处】
无
【标注】
【答案】
延长 $BD$ 到 $E$,使得 $DE=CD$,连接 $AE$.
因为 $\angle ADB=90^\circ-\dfrac 12\angle BDC$,
所以 $2\angle ADB+\angle BDC=180^\circ$,即 $\angle ADC+\angle ADB=180^\circ$.
因为 $\angle ADE+\angle ADB=180^\circ$,
所以 $\angle ADC=\angle ADE$.
因为 $CD=DE$,$AD=AD$,
所以 $\triangle ADC\cong \triangle ADE,$
所以 $\angle ACD=\angle E=60^\circ$,$AC=AE$.
因为 $\angle ACD=\angle ABD=60^\circ$,
所以 $\angle ABD=\angle E$,
所以 $AB=AE$,
所以 $AB=AC$,
所以 $\triangle ABC$ 是等腰三角形.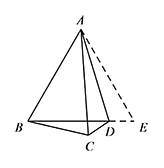
因为 $\angle ADB=90^\circ-\dfrac 12\angle BDC$,
所以 $2\angle ADB+\angle BDC=180^\circ$,即 $\angle ADC+\angle ADB=180^\circ$.
因为 $\angle ADE+\angle ADB=180^\circ$,
所以 $\angle ADC=\angle ADE$.
因为 $CD=DE$,$AD=AD$,
所以 $\triangle ADC\cong \triangle ADE,$
所以 $\angle ACD=\angle E=60^\circ$,$AC=AE$.
因为 $\angle ACD=\angle ABD=60^\circ$,
所以 $\angle ABD=\angle E$,
所以 $AB=AE$,
所以 $AB=AC$,
所以 $\triangle ABC$ 是等腰三角形.
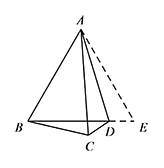
【解析】
略
答案
解析
备注