设 $M$ 是凸四边形 $ABCD$ 的边 $BC$ 的中点，$\angle AMD=135^\circ$，求证：$AB+\dfrac{\sqrt 2}{2}BC+CD\geqslant AD$．
【难度】
【出处】
无
【标注】
【答案】
如图，将 $\triangle ABM$ 沿 $AM$ 翻折得到 $\triangle AB'M$，将 $\triangle CDM$ 沿 $DM$ 翻折得到 $\triangle C'DM$，连接 $B'C'$．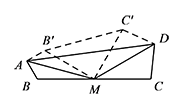
则 $MB'=MB=MC=MC'$，
$\angle B'MC'=\angle AMD-\angle AMB-\angle DMC=90^\circ$，
从而 $B'C'=\sqrt 2MB=\dfrac {\sqrt 2}2BC$，
所以 $AB+\dfrac{\sqrt 2}2BC+CD=AB'+B'C'+C'D\geqslant AD$
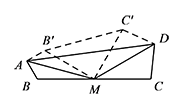则 $MB'=MB=MC=MC'$，$\angle B'MC'=\angle AMD-\angle AMB-\angle DMC=90^\circ$，
从而 $B'C'=\sqrt 2MB=\dfrac {\sqrt 2}2BC$，
所以 $AB+\dfrac{\sqrt 2}2BC+CD=AB'+B'C'+C'D\geqslant AD$
【解析】
略
答案
解析
备注
