如图,已知两条抛物线 $E_1:y^2=2p_1x$($p_1>0$)和 $E_2:y^2=2p_2x$($p_2>0$),过原点 $O$ 的两条直线 $l_1$ 和 $l_2$,$l_1$ 与 $E_1,E_2$ 分别交于 $A_1,A_2$ 两点,$l_2$ 与 $E_1,E_2$ 分别交于 $B_1,B_2$ 两点.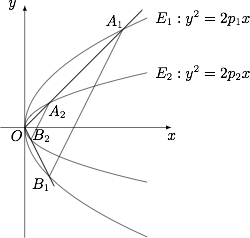

【难度】
【出处】
2014年高考安徽卷(理)
【标注】
-
证明:$A_1B_1 \parallel A_2B_2$;标注答案略解析设 $A_1(2p_1t_1^2,2p_1t_1)$,$B_1(2p_1t_2^2,2p_1t_2)$,$A_2(2p_2t_3^2,2p_2t_3)$,$B_2(2p_2t_4^2,2p_2t_4)$.
由 $A_1,A_2,O$ 三点共线,有直线 $OA_1$ 与直线 $OA_2$ 的斜率相等,从而 $t_1=t_3$;类似的,由 $B_1,B_2,O$ 三点共线,可得 $t_2=t_4$.
当 $t_1+t_2\neq 0$ 时,直线 $A_1B_1$ 的斜率为$$\dfrac{2p_1t_1-2p_1t_2}{2p_1t_1^2-2p_1t_2^2}=\dfrac{1}{t_1+t_2},$$同理可得直线 $A_2B_2$ 的斜率为 $\dfrac{1}{t_3+t_4}$,因此 $A_1B_1\parallel A_2B_2$.
当 $t_1+t_2=0$ 时,$t_3+t_4=0$,因此直线 $A_1B_1$ 与直线 $A_2B_2$ 均垂直于 $x$ 轴,此时仍有 $A_1B_1\parallel A_2B_2$.
综上,原命题得证. -
过 $O$ 作直线 $l$(异于 $l_1,l_2$)与 $E_1,E_2$ 分别交于 $C_1,C_2$ 两点.记 $\triangle A_1B_1C_1$ 与 $\triangle A_2B_2C_2$ 的面积分别为 $S_1$ 与 $S_2$,求 $\dfrac{S_1}{S_2}$ 的值.标注答案$\dfrac{S_1}{S_2}=\dfrac{p_1^2}{p_2^2}$解析由第 $(1)$ 小题的结论可知,$\triangle A_1B_1C_1$ 与 $\triangle A_2B_2C_2$ 的三边分别平行,因此三个内角对应相等,于是 $\triangle A_1B_1C_1$ 与 $\triangle A_2B_2C_2$ 相似,其面积比 $\dfrac{S_1}{S_2}=\left(\dfrac{A_1B_1}{A_2B_2}\right)^2$,又 $\triangle OA_1B_1$ 与 $\triangle OA_2B_2$ 相似,因此$$\dfrac{A_1B_1}{A_2B_2}=\dfrac{OA_1}{OA_2}=\dfrac{2p_1t_1}{2p_2t_3}=\dfrac{p_1}{p_2},$$这样我们就有 $\dfrac{S_1}{S_2}=\dfrac{p_1^2}{p_2^2}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2