题目 设函数 $f\left(x\right) = \dfrac{1}{{\sqrt {{{\left({x^2} + 2x + k\right)}^2} + 2\left({x^2} + 2x + k\right) - 3} }}$，其中 $k < - 2$． 问题1 求函数 $f\left(x\right)$ 的定义域 $D$（用区间表示）； 答案1 函数 $y=f(x)$ 的定义域为 $(-\infty ,x_1)\cup (x_3,x_4)\cup (x_2,+\infty ),$ 其中$$\begin{split} x_1=&-1-\sqrt{2-k},x_2=-1+\sqrt{2-k},\\x_3=&-1-\sqrt{-2-k},x_4=-1+\sqrt{-2-k}.\end{split}$$ 解析1 函数 $y=f(x)$ 可以看作是三个函数$$y=\dfrac{1}{\sqrt{u}},u=t^2+2t-3,t=x^2+2x+k$$复合形成的函数．<br/>函数 $y=\dfrac{1}{\sqrt{u}}$ 的定义域为 $\{u|u>0\}$，于是 $t$ 的取值范围是 $\left\{t\left|t<-3\lor t>1\right.\right\}$，因此函数 $y=f(x)$ 的定义域为$$\left\{x<br/>\mid x^2+2x+k<-3\lor x^2+2x+k>1\right\}$$即$$\left\{x\mid x^2+2x+k+3<0\lor x^2+2x+k-1>0\right\}.$$由于 $k<-2$，因此可设关于 $x$ 的方程 $x^2+2x+k-1=0$ 的两根分别为 $x_1,x_2$（$x_1<x_2$），关于 $x$ 的方程 $x^2+2x+k+3=0$ 的两根分别为 $x_3,x_4$（$x_3<x_4$），则$$\begin{split} x_1=&-1-\sqrt{2-k},x_2=-1+\sqrt{2-k},\\x_3=&-1-\sqrt{-2-k},x_4=-1+\sqrt{-2-k},\end{split}$$于是函数 $y=f(x)$ 的定义域为 $(-\infty ,x_1)\cup (x_3,x_4)\cup (x_2,+\infty )$． 备注1 问题2 讨论函数 $f\left(x\right)$ 在 $D$ 上的单调性； 答案2 略 解析2 注意到函数 $t=x^2+2x+k$ 的对称轴为 $x=-1$，最小值为 $k-1$，因此将定义域分段讨论如下．$$\begin{array}{|c|c|c|c|c|}\hline x&(-\infty,x_1)&(x_3,-1)&(-1,x_4)&(x_2,+\infty)\\ \hline t_x&\searrow&\searrow&\nearrow&\nearrow\\ \hline t&(1,+\infty)&(k-1,-3)&(k-1,-3)&(1,+\infty)\\ \hline u_t&\nearrow&\searrow&\searrow&\nearrow\\ \hline u_x&\searrow&\nearrow&\searrow&\nearrow\\ \hline\end{array}$$其中 $t_x=x^2+2x+k$，$u_t=t^2+2t-3$，$u_x=(x^2+2x+k)^2+2(x^2+2x+k)-3$．<br/>又由于 $y=\dfrac{1}{\sqrt{u}}$ 始终为单调递减函数，因此 $f(x)$ 在区间 $(-\infty,x_1)$ 上单调递增，在区间 $(x_3,-1)$ 上单调递减，在区间 $(-1,x_4)$ 上单调递增，在区间 $(x_2,+\infty )$ 上单调递减，其中$$\begin{split} x_1=&-1-\sqrt{2-k},x_2=-1+\sqrt{2-k},\\x_3=&-1-\sqrt{-2-k},x_4=-1+\sqrt{-2-k}.\end{split}$$ 备注2 问题3 若 $k < - 6$，求 $D$ 上满足条件 $f\left(x\right) > f\left(1\right)$ 的 $x$ 的集合（用区间表示）． 答案3 不等式 $f(x)>f(1)$ 的解集为 $(x_5,x_1)\cup(x_3,-3)\cup(1,x_4)\cup(x_2,x_6)$，其中\[\begin{split} &x_1=-1-\sqrt{2-k},x_2=-1+\sqrt{2-k},\\&x_3=-1-\sqrt{-2-k},x_4=-1+\sqrt{-2-k},\\&x_5=-1-\sqrt{-2k-4},x_6=-1+\sqrt{-2k-4}.\end{split}\] 解析3 条件 $f(x)>f(1)$ 即$$(x^2+2x+k)^2+2(x^2+2x+k)-3<(k+3)^2+2(k+3)-3,$$也即$$(x^2+2x+k+k+3)(x^2+2x+k-k-3)+2(x^2+2x+k-k-3)<0,$$整理得$$(x^2+2x+2k+5)(x^2+2x-3)<0.$$由于 $k<-6$，于是方程 $x^2+2x+2k+5=0$ 的两根 $x_5,x_6$（$x_5<x_6$）分别在区间 $(-\infty ,x_1),(x_2,+\infty )$ 上．同时方程 $x^2+2x-3=0$ 的两根 $x_7,x_8$（$x_7<x_8$）均在区间 $(x_3,x_4)$ 上，且$$x_5=-1-\sqrt{-2k-4},x_6=-1+\sqrt{-2k-4},x_7=-3,x_8=1.$$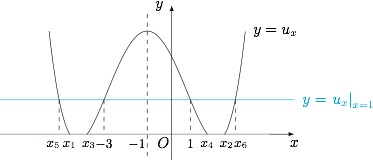<img src="/static/images/e1dc0a859805027ee5aa266311f5f455.png" class="img-responsive" />结合函数 $u_x$ 的定义域以及单调性可知不等式 $f(x)>f(1)$ 的解集为 $(x_5,x_1)\cup(x_3,-3)\cup(1,x_4)\cup(x_2,x_6)$，其中\[\begin{split} &x_1=-1-\sqrt{2-k},x_2=-1+\sqrt{2-k},\\&x_3=-1-\sqrt{-2-k},x_4=-1+\sqrt{-2-k},\\&x_5=-1-\sqrt{-2k-4},x_6=-1+\sqrt{-2k-4}.\end{split}\] 备注3