已知 $x,y,z\geqslant 0$，且 $x+y+z=6$，求 $\sqrt{x^2+4}+\sqrt{y^2+9}+\sqrt{z^2+16}$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$\left[3\sqrt{13},7+2\sqrt{10}\right]$
【解析】
如图，作 $6\times 9$ 的矩形 $ABCD$，并画两条横线 $EF,GH$ 将矩形长度为 $9$ 的边分为 $2,3,4$ 的三段．在两条横线上分别依次选取 $M,N$ 两点，则$$AM+MN+NC=\sqrt{x^2+4}+\sqrt{y^2+9}+\sqrt{z^2+16}.$$
不难证明$$AC\leqslant AM+MN+NC\leqslant AF+FH+HC,$$因此所求的取值范围是 $\left[3\sqrt{13},7+2\sqrt{10}\right]$．
下面来证明 $AF+FH+HC$ 最长．先给出一个引理：
引理 在 $\triangle ABC$ 中，在 $\triangle ABC$ 的内部从 $B$ 到 $C$ 有一条凸的路线 $B-D_1-D_2-\cdots-D_n-C$（即多边形 $BCD_nD_{n-1}\cdots D_1$ 是凸多边形），那么有凸多边形的周长小于三角形的周长，也即$$BD_1+D_1D_2+\cdots+D_nC<AB+AC.$$证明 以 $n=2$ 为例证明，分别延长 $BD_1,D_1D_2$ 交边 $AC$ 于点 $E_1,E_2$，如图：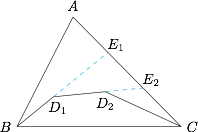
则有$$\begin{cases} AB+AE_1>BD_1+D_1E_1,\\D_1E_1+E_1E_2>D_1D_2+D_2E_2,\\D_2E_2+EC>D_2C,\end{cases}$$左右两边分别相加得 $AB+AC>BD_1+D_1D_2+D_2C$．
回到本题 固定 $M$ 点，由引理知，从 $MN+NC$ 的最大值是点 $N$ 在最右边（与点 $H$ 重合）或者最左边（与点 $M$ 在 $GH$ 上的射影重合）时取到，比较这两个值知，点 $N$ 在最右边；同理，当 $N$ 固定时，点 $M$ 在最右边时，$AM+MN$ 有最大值．所以当 $M$ 在 $F$ 处，$N$ 在 $H$ 处时有最大值．
不难证明$$AC\leqslant AM+MN+NC\leqslant AF+FH+HC,$$因此所求的取值范围是 $\left[3\sqrt{13},7+2\sqrt{10}\right]$．下面来证明 $AF+FH+HC$ 最长．先给出一个引理：
则有$$\begin{cases} AB+AE_1>BD_1+D_1E_1,\\D_1E_1+E_1E_2>D_1D_2+D_2E_2,\\D_2E_2+EC>D_2C,\end{cases}$$左右两边分别相加得 $AB+AC>BD_1+D_1D_2+D_2C$．
答案
解析
备注
