已知 $\triangle ABC$ 内一点 $D$ 满足 $\angle BAD=\angle BCD$，且 $\angle BDC=90^\circ$．已知 $AB=5$，$BC=6$，$M$ 为 $AC$ 中点，求 $DM$．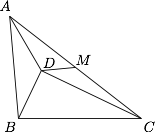
【难度】
【出处】
无
【标注】
【答案】
$\dfrac {\sqrt {11}}2$
【解析】
作 $\triangle BDC$ 的外接圆，并将 $\triangle BDC$ 连同外接圆一起关于 $BD$ 对称，设 $C$ 的对应点为 $C'$．
由于 $\angle BAD=\angle BCD$，于是 $A$ 点对称圆上且 $D$ 为 $CC'$ 的中点．于是$$DM=\dfrac 12AC'=\dfrac 12\sqrt{BC'^2-AB^2}=\dfrac 12\sqrt{BC^2-AB^2}=\dfrac {\sqrt {11}}2.$$
由于 $\angle BAD=\angle BCD$，于是 $A$ 点对称圆上且 $D$ 为 $CC'$ 的中点．于是$$DM=\dfrac 12AC'=\dfrac 12\sqrt{BC'^2-AB^2}=\dfrac 12\sqrt{BC^2-AB^2}=\dfrac {\sqrt {11}}2.$$
答案
解析
备注
