如图，在平面直角坐标系 $xOy$ 中，${F_1}$，${F_2}$ 分别是椭圆 $\dfrac{x^2}{a^2}+ \dfrac{y^2}{b^2}= 1 \left(a > b > 0\right)$ 的左、右焦点，顶点 $B$ 的坐标为 $\left(0,b\right)$，连接 $B{F_2}$ 并延长交椭圆于点 $A$，过点 $A$ 作 $x$ 轴的垂线交椭圆于另一点 $C$，连接 ${F_1}C$．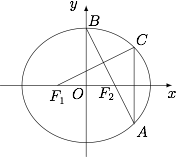
【难度】
【出处】
2014年高考江苏卷
【标注】
-
若点 $C$ 的坐标为 $\left(\dfrac{4}{3},\dfrac{1}{3}\right)$，且 $B{F_2}= \sqrt 2$，求椭圆的方程；标注答案$\dfrac{x^2}{2}+y^2=1$解析根据题意，$BF_2=a=\sqrt 2$，又$$\dfrac{1}{a^2}\cdot\left(\dfrac 43\right)^2+\dfrac{1}{b^2}\cdot\left(\dfrac 13\right)^2=1,$$从而 $b=1$，因此椭圆的方程为 $\dfrac{x^2}{2}+y^2=1$．
-
若 ${F_1}C \perp AB$，求椭圆离心率 $e$ 的值．标注答案$\dfrac{\sqrt 5}5$解析如图，连接 $BF_1$，$AF_1$．
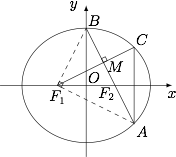记 $\angle F_1BO=\theta$，则 $\angle OBF_2=\angle OF_1M=\angle AF_1F_2=\theta$，于是$$\angle BF_1A=\angle BF_1M+2\theta=90^\circ.$$在直角三角形 $ABF_1$ 中，设 $AF_2=m$，则 $BF_1=a$，$BA=BF_2+AF_2=a+m$，$AF_1=2a-AF_2=2a-m$，由勾股定理得$$AB^2=AF_1^2+BF_1^2,$$从而$$(a+m)^2=(2a-m)^2+a^2,$$解得 $m=\dfrac 23a$，因此 $\cos 2\theta=\dfrac{BF_1}{BA}=\dfrac 35$，进而$$e=\dfrac ca=\dfrac{OF_1}{BF_1}=\sin\theta=\sqrt{\dfrac{1-\cos 2\theta}2}=\dfrac{\sqrt 5}5.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
