如图，已知抛物线 $C:{x^2}= 4y$，过点 $M\left(0,2\right)$ 任作一直线与 $C$ 相交于 $A$，$B$ 两点，过点 $B$ 作 $y$ 轴的平行线与直线 $AO$ 相交于点 $D$（$O$ 为坐标原点）．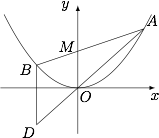
【难度】
【出处】
2014年高考江西卷（文）
【标注】
-
证明：动点 $D$ 在定直线上；标注答案略解析设 $A(4t_1,4t_1^2)$，$B(4t_2,4t_2^2)$，$D(4t_2,m)$．
由于 $A,M,B$ 三点共线，从而$$\dfrac{4t_1^2-2}{4t_1-0}=\dfrac{4t_2^2-2}{4t_2-0},$$整理可得 $t_1t_2=-\dfrac 12.$
由于 $A,O,D$ 三点共线，从而$$\dfrac{4t_1^2}{4t_1}=\dfrac{m}{4t_2},$$于是 $m=4t_1t_2=-2$ 为定值，因此动点 $D$ 在定直线 $y=-2$ 上． -
作 $C$ 的任意一条切线 $l$（不含 $x$ 轴）与直线 $y = 2$ 相交于点 ${N_1}$，与 $(1)$ 中的定直线相交于点 ${N_2}$，证明：${\left|{M{N_2}}\right|}^2 - |M{N_1}|^2$ 为定值，并求此定值．标注答案$|MN_2|^2-|MN_1|^2$ 为定值 $8$解析根据题意，作示意图．
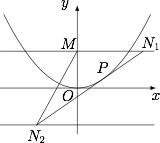设 $P(4t,4t^2)$，则抛物线 $y=\dfrac 14x^2$ 在 $x=4t$ 处的切线方程为$$y=2t(x-4t)+4t^2,$$即 $y=2tx-4t^2$．
分别与直线 $y=2$ 和 $y=-2$ 联立，可得 $N_1\left(2t+\dfrac 1t,2\right)$，$N_2\left(2t-\dfrac 1t,-2\right)$，因此$$|MN_2|^2-|MN_1|^2=\left(2t-\dfrac 1t\right)^2+16-\left(2t+\dfrac 1t\right)^2=8,$$因此 $|MN_2|^2-|MN_1|^2$ 为定值 $8$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
