设点 $M$ 为椭圆 $C:\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1(a>b>0)$ 上的一动点，$A,B$ 分别为椭圆的左，右顶点．求证：当且仅当 $M$ 是椭圆的上顶点或下顶点时 $\triangle MAB$ 周长和面积取得最大值．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
由于 $|AB|$ 为定值 $2a$，因此当 $M$ 是椭圆的上顶点或下顶点时，视 $AB$ 为底边，$\triangle MAB$ 的高最大，此时面积取得最大值．下面证明当 $M$ 是椭圆的上顶点或下顶点时 $|MA|+|MB|$ 最大．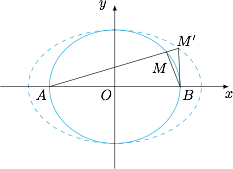
以 $2\sqrt{a^{2}+b^{2}}$ 为长轴长，$A,B$ 为焦点作椭圆，则椭圆方程为 $C':\dfrac{x^{2}}{a^{2}+b^{2}}+\dfrac{y^{2}}{b^{2}}=1$．容易证明除椭圆 $C$ 的上下顶点外，椭圆 $C$ 在椭圆 $C'$ 内部，因此\[|MA|+|MB|\leqslant |M'A|+|M'B|,\]当且仅当 $M$ 为椭圆 $C$ 的上下顶点时取得等号．因此原命题成立．
以 $2\sqrt{a^{2}+b^{2}}$ 为长轴长，$A,B$ 为焦点作椭圆，则椭圆方程为 $C':\dfrac{x^{2}}{a^{2}+b^{2}}+\dfrac{y^{2}}{b^{2}}=1$．容易证明除椭圆 $C$ 的上下顶点外，椭圆 $C$ 在椭圆 $C'$ 内部，因此\[|MA|+|MB|\leqslant |M'A|+|M'B|,\]当且仅当 $M$ 为椭圆 $C$ 的上下顶点时取得等号．因此原命题成立．
答案
解析
备注
