题目 已知函数 $f\left(x\right) ={{\mathrm{e}}^x}- a{x^2}- bx - 1$，其中 $a,b \in{\mathbb{R}}$，${\mathrm{e}}= 2.71828 \cdots$ 为自然对数的底数． 问题1 设 $g\left(x\right)$ 是函数 $f\left(x\right)$ 的导函数，求函数 $g\left(x\right)$ 在区间 $\left[0,1\right]$ 上的最小值； 答案1 函数 $g(x)$ 在区间 $[0,1]$ 上的最小值$$\min_{x\in[0,1]}g(x)=\begin{cases} 1-b,a\leqslant \dfrac 12,\\2a-2a\ln(2a)-b,\dfrac 12<a<\dfrac{\rm e}2,\\{\rm e}-2a-b,a\geqslant \dfrac{\rm e}2.\end{cases}$$ 解析1 根据题意，$g(x)={\rm e}^x-2ax-b$，于是其导函数$$g'(x)={\rm e}^x-2a,$$于是当 $a\leqslant \dfrac 12$ 时，函数 $g(x)$ 在区间 $[0,1]$ 上单调递增，其最小值为 $g(0)=1-b$；<br/>当 $\dfrac 12 < a < \dfrac {\rm e}{2}$ 时，函数 $g(x)$ 在区间 $[0,1]$ 上先单调递减，再单调递增，其最小值为$$g(\ln (2a))=2a-2a\ln(2a)-b;$$当 $a\geqslant \dfrac {\rm e}2$ 时，函数 $g(x)$ 在区间 $[0,1]$ 上单调递减，其最小值为 $g(1)={\rm e}-2a-b$．<br/>因此函数 $g(x)$ 在区间 $[0,1]$ 上的最小值$$\min_{x\in[0,1]}g(x)=\begin{cases} 1-b,a\leqslant \dfrac 12,\\2a-2a\ln(2a)-b,\dfrac 12<a<\dfrac{\rm e}2,\\{\rm e}-2a-b,a\geqslant \dfrac{\rm e}2.\end{cases}$$ 备注1 问题2 若 $f\left(1\right) = 0$，函数 $f\left(x\right)$ 在区间 $\left(0,1\right)$ 内有零点，求 $a$ 的取值范围． 答案2 $({\rm e}-2,1)$ 解析2 一方面，注意到 $f(0)=f(1)=0$，因此函数 $f(x)$ 在区间 $[0,1]$ 内至少有 $3$ 个零点，因此其导函数 $f'(x)$ 在 $(0,1)$ 上至少有 $2$ 个零点；<br/>另一方面，函数 $f''(x)$ 为单调递增函数，因此 $f'(x)$ 至多有 $2$ 个零点；<br/>综合以上两方面，可得函数 $f'(x)$ 在 $(0,1)$ 上有 $2$ 个零点为函数 $f(x)$ 在区间 $[0,1]$ 内有 $3$ 个零点的充要条件．如果我们将 $f'(x)$ 在 $(0,1)$ 上的零点看作是指数函数 $y={\rm e}^x$ 的图象与直线 $y=2ax+b$ 的交点横坐标，那么条件 $f(1)=0$ 即 $a+b={\rm e}-1$ 意味着直线 $y=2ax+b$ 过定点 $P\left(\dfrac 12,{\rm e}-1\right)$，如图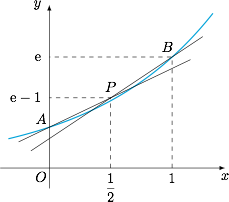．<img src="/static/images/cad00f300fd8a4163add6a3ae68af4d7.png" class="img-responsive" />$P$ 点在指数函数 $y={\rm e}^x$ 图象的上方，记 $A(0,1)$，$B(1,{\rm e})$，则指数函数 $y={\rm e}^x$ 的图象与直线 $y=2ax+b$ 有 $2$ 个交点等价于直线斜率 $2a$ 在直线 $PA$ 的斜率和直线 $PB$ 的斜率之间．不难计算得 $a$ 的取值范围为 $({\rm e}-2,1)$． 备注2