已知椭圆 $E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$（$a>b>0$）所在平面内有一个不与原点重合的点 $P(x_0,y_0)$，过 $P$ 作 $E$ 的任意两条割线 $AB,CD$，其中 $A,B,C,D$ 均在椭圆 $E$ 上．证明：直线 $AC$ 和 $BD$ 的交点在定直线上．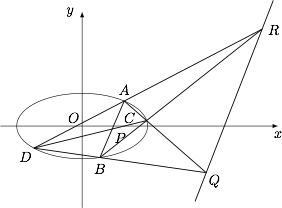
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
如图，设直线 $AC$ 与 $BD$ 的交点为 $Q$，直线 $AD$ 与 $BC$ 的交点为 $R$，则直线 $RQ$ 即题中的定直线．
如图，设直线 $AB,CD$ 分别与直线 $RQ$ 相交于 $S,T$，则利用完全四边形 $ABCD$ 可得四点 $S,R,T,Q$ 为共线的调和点列．下面证明直线 $SRTQ$ 由 $P$ 点位置确定，与直线 $AB$ 和 $CD$ 的作法无关．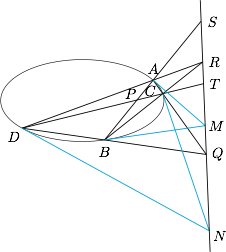
在 $A,B$ 处作切线，两条切线交于 $M$；在 $C,D$ 处作切线，两条切线交于 $N$．根据帕斯卡（Pascal）定理，$M,N$ 均在直线 $ST$ 上，即 $S,R,T,Q,M,N$ 六点共线．但从图中可以看出，$S,M$ 两点只和直线 $AB$ 有关，与直线 $CD$ 完全无关，所以我们将直线 $AB$ 换成任意的另一条直线 $A'B'$，只要 $A'B'$ 通过点 $P$，则形成的 $S,Q,T,Q$ 四点仍与 $M,N$ 共线．类似的，可以证明直线 $SRTQ$ 的位置与直线 $AB$ 完全无关，而只取决于 $P$ 点位置，因此原命题得证．
如图，设直线 $AB,CD$ 分别与直线 $RQ$ 相交于 $S,T$，则利用完全四边形 $ABCD$ 可得四点 $S,R,T,Q$ 为共线的调和点列．下面证明直线 $SRTQ$ 由 $P$ 点位置确定，与直线 $AB$ 和 $CD$ 的作法无关．
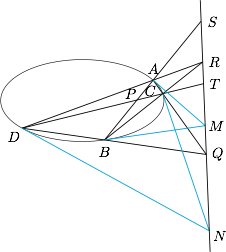在 $A,B$ 处作切线，两条切线交于 $M$；在 $C,D$ 处作切线，两条切线交于 $N$．根据帕斯卡（Pascal）定理，$M,N$ 均在直线 $ST$ 上，即 $S,R,T,Q,M,N$ 六点共线．但从图中可以看出，$S,M$ 两点只和直线 $AB$ 有关，与直线 $CD$ 完全无关，所以我们将直线 $AB$ 换成任意的另一条直线 $A'B'$，只要 $A'B'$ 通过点 $P$，则形成的 $S,Q,T,Q$ 四点仍与 $M,N$ 共线．类似的，可以证明直线 $SRTQ$ 的位置与直线 $AB$ 完全无关，而只取决于 $P$ 点位置，因此原命题得证．
答案
解析
备注
