平面直角坐标系 $xOy$ 中，已知椭圆 $C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$ 的离心率为 $\dfrac{\sqrt 3}2$，左、右焦点分别是 $F_1$、$F_2$．以 $F_1$ 为圆心，以 $3$ 为半径的圆与以 $F_2$ 为圆心，以 $1$ 为半径的圆相交，且交点在椭圆 $C$ 上．
【难度】
【出处】
无
【标注】
-
求椭圆 $C$ 的方程；标注答案$\dfrac{x^2}4+y^2=1$解析显然椭圆 $C$ 的长轴长为 $4$，于是方程为 $\dfrac{x^2}4+y^2=1$．
-
设椭圆 $E:\dfrac{x^2}{4a^2}+\dfrac{y^2}{4b^2}=1$，$P$ 为椭圆 $C$ 上任意一点，过点 $P$ 的直线 $y=kx+m$ 交椭圆 $E$ 于 $A$、$B$ 两点，射线 $PO$ 交椭圆 $E$ 于点 $Q$．
① 求 $\dfrac{|OQ|}{|OP|}$ 的值；
② 求 $\triangle ABQ$ 面积的最大值．标注答案① $2$；② $6\sqrt 3$解析① $2$；
② 如图，将椭圆 $C$ 和椭圆 $E$ 伸缩变换为圆 $C':x^2+y^2=4$ 和圆 $E':x^2+y^2=16$．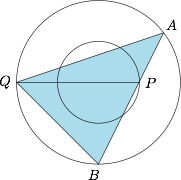
设变换后 $AB$ 与 $PQ$ 所成角为 $\theta$，原点 $O$ 到直线 $AB$ 距离为 $d$，则\[S_{\triangle QAB}=\dfrac 12\sin\theta \cdot AB\cdot PQ=\dfrac 12 \cdot \dfrac{d}2\cdot 2\sqrt{4^2-d^2}\cdot 6=3\sqrt{d^2\left(16-d^2\right)},\]由于 $0\leqslant d^2\leqslant 4$，于是当 $d^2=4$ 时，三角形 $QAB$ 的面积取得最大值为 $12\sqrt 3$．于是变换前三角形 $QAB$ 面积的最大值为 $6\sqrt 3$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
