题目 已知函数 $f(x)=\dfrac 23x+\dfrac 12$，$h(x)=\sqrt x$． 问题1 设函数 $F(x)=f(x)-h(x)$，求 $F(x)$ 的单调区间与极值； 答案1 $F(x)$ 的单调递减区间是 $\left(0,\dfrac {9}{16}\right)$，单调递增区间是 $\left(\dfrac{9}{16},+\infty\right)$．当 $x=\dfrac{9}{16}$ 时，函数 $F(x)$ 取得极小值 $\dfrac 18$，函数 $F(x)$ 没有极大值 解析1 函数 $F(x)$ 的导函数$$F'(x)=\dfrac{4\sqrt x-3}{6\sqrt x},x>0,$$于是 $F(x)$ 的单调递减区间是 $\left(0,\dfrac {9}{16}\right)$；$F(x)$ 单调递增区间是 $\left(\dfrac{9}{16},+\infty\right)$．当 $x=\dfrac{9}{16}$ 时，函数 $F(x)$ 取得极小值 $\dfrac 18$，函数 $F(x)$ 没有极大值． 备注1 问题2 设 $a\in\mathbb R$，解关于 $x$ 的方程 ${\log_4}\left[\dfrac 32f(x-1)-\dfrac 34\right]={\log_2}h(a-x)-{\log_2}h(4-x)$； 答案2 当 $1<a\leqslant 4$ 或 $a=5$ 时，原方程有一解 $x=3-\sqrt {5-a}$；<br/>$4<a<5$ 时，原方程有两解 $x=3\pm\sqrt{5-a}$；<br/>当 $a\leqslant 1$ 或 $a>5$ 时，原方程无解 解析2 原方程等价于$$\dfrac 12{\log_2}(x-1)+{\log_2}\sqrt{4-x}={\log_2}\sqrt{a-x},$$即$$\begin{cases} 1<x<4,\\ x<a,\\ a=-x^2+6x-4,\end{cases}$$画出函数 $y=-x^2+6x-4$ 和 $y=x$ 的图象，如图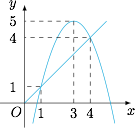．<img src="/static/images/58d1153dd1c266faa85e147be422dc65.png" class="img-responsive" />于是可得，当 $1<a\leqslant 4$ 或 $a=5$ 时，原方程有一解 $x=3-\sqrt {5-a}$；$4<a<5$ 时，原方程有两解 $x=3\pm\sqrt{5-a}$；当 $a\leqslant 1$ 或 $a>5$ 时，原方程无解． 备注2 问题3 试比较 $\displaystyle f(100)h(100)-\sum_{k=1}^{100}h(k)$ 与 $\dfrac 16$ 的大小． 答案3 $\displaystyle f(100)h(100)-\sum_{k=1}^{100}h(k)>\dfrac 16$ 解析3 令 $\displaystyle S_n=f(n)h(n)-\sum_{k=1}^{n}h(k),n\in\mathbb N^*$，则 $S_1=f(1)h(1)-1=\dfrac 16$，且\[\begin{split} S_{n+1}-S_n&=\left[\dfrac 23(n+1)+\dfrac 12\right]\cdot\sqrt{n+1}-\left(\dfrac 23n+\dfrac 12\right)\cdot \sqrt n-\sqrt{n+1}\\<br/>&=\dfrac 16\left[(4n+1)\sqrt{n+1}-(4n+3)\sqrt{n}\right]\\<br/>&=\dfrac 16\left[\sqrt{16n^3+24n^2+9n+1}-\sqrt{16n^3+24n^2+9n}\right]\\<br/>&>0,\end{split}\]于是数列 $\{S_n\}$ 是单调递增数列，因此 $S_{100}>S_1=\dfrac 16$． 备注3