设椭圆 $\dfrac{x^2}{a^2}+ \dfrac{y^2}{b^2}= 1$（$a > b > 0$）的左、右焦点分别为 ${F_1},{F_2}$，右顶点为 $A$，上顶点为 $B$，已知 $\left|{AB}\right| = \dfrac{\sqrt 3}{2}\left|{{F_1}{F_2}}\right|$．
【难度】
【出处】
2014年高考天津卷（理）
【标注】
-
求椭圆的离心率；标注答案$\dfrac{\sqrt 2}2$解析设椭圆的半焦距为 $c$，则根据题意有$$\sqrt{a^2+b^2}=\dfrac{\sqrt 3}2\cdot 2c,$$又 $a^2=b^2+c^2$，因此 $a^2=2c^2$，椭圆的离心率 $e=\dfrac ca=\dfrac{\sqrt 2}2$．
-
设 $P$ 为椭圆上异于其顶点的一点，以线段 $PB$ 为直径的圆经过点 ${F_1}$，经过原点 $O$ 的直线 $l$ 与该圆相切．求直线 $l$ 的斜率．标注答案$4\pm \sqrt{15}$解析画出示意图，如图．
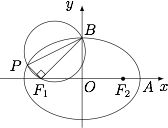根据题意，$BF_1\perp PF_1$，因此由直线 $BF_1$ 的斜率为 $1$ 可得直线 $PF_1$ 的斜率为 $-1$，不妨设 $F_1(-1,0)$，则有直线 $PF_1$ 的方程为 $x=-y-1$，椭圆方程为 $\dfrac{x^2}2+y^2=1$，联立得$$3y^2+2y-1=0,$$于是 $y=-1$（舍去，因为点 $P$ 不为椭圆的顶点）或 $y=\dfrac 13$．
当 $y=\dfrac 13$ 时，可得 $P\left(-\dfrac 43,\dfrac 13\right)$，因此圆的圆心为 $\left(-\dfrac 23,\dfrac 23\right)$，半径为 $\sqrt{\dfrac 59}$．由于直线 $x=0$ 不与该圆相切，因此设直线 $l$ 的方程为 $y=kx$，有$$\dfrac{\left|-\dfrac 23k-\dfrac 23\right|}{\sqrt{1+k^2}}=\sqrt{\dfrac 59},$$解得 $k=4\pm \sqrt{15}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
