题目 已知函数 $f\left(x\right) ={x^2}- \dfrac{2}{3}a{x^3}\left(a > 0\right)$，$x \in{\mathbb{R}}$． 问题1 求 $f\left(x\right)$ 的单调区间和极值； 答案1 函数 $f(x)$ 的单调递增区间是 $\left(0,\dfrac 1a\right)$，单调递减区间是 $(-\infty ,0)$ 和 $\left(\dfrac 1a,+\infty \right)$；极大值为 $f\left(\dfrac 1a\right)=\dfrac{1}{3a^2}$，极小值为 $f(0)=0$ 解析1 函数 $f(x)$ 的导函数$$f'(x)=2ax\left(\dfrac 1a-x\right),$$因此函数 $f(x)$ 在 $(-\infty ,0)$ 上单调递减，在 $\left(0,\dfrac 1a\right)$ 上单调递增，在 $\left(\dfrac 1a,+\infty \right)$ 上单调递减，在 $x=0$ 处取极小值 $f(0)=0$，在 $x=\dfrac 1a$ 处取极大值 $f\left(\dfrac 1a\right)=\dfrac{1}{3a^2}$．<br/>因此函数 $f(x)$ 的单调递增区间是 $\left(0,\dfrac 1a\right)$，单调递减区间是 $(-\infty ,0)$ 和 $\left(\dfrac 1a,+\infty \right)$；极大值为 $f\left(\dfrac 1a\right)=\dfrac{1}{3a^2}$，极小值为 $f(0)=0$． 备注1 问题2 若对于任意的 ${x_1}\in \left(2, + \infty \right)$，都存在 ${x_2}\in \left(1, + \infty \right)$，使得 $f\left({x_1}\right) \cdot f\left({x_2}\right) = 1$，求 $a$ 的取值范围． 答案2 $\left[\dfrac 34,\dfrac 32\right]$ 解析2 函数 $f(x)$ 的零点为 $x=0$ 和 $x=\dfrac{3}{2a}$，图象如图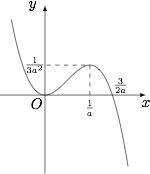．<img src="/static/images/6e5940b91b258be6e22025edef5dd1ef.png" class="img-responsive" />显然 $2\geqslant \dfrac{3}{2a}$，即 $a\geqslant \dfrac 34$，否则取 $x_1=\dfrac{3}{2a}$，$f(x_1)\cdot f(x_2)=0$，不符合题意；<br/>当 $a=\dfrac 34$ 时，由于 $f(x_1)$ 的取值范围是 $(-\infty ,0)$，而 $f(x_2)$ 可以取遍所有负实数，因此符合题意；<br/>当 $a>\dfrac 34$ 时，问题转化为函数 $f(x)$ 在 $(1,+\infty )$ 上的值域包含$$\left\{\left.\dfrac{1}{f(x_1)}\right|x_1>2\right\}=\left(\dfrac{1}{f(2)},0\right),$$于是 $1\leqslant \dfrac{3}{2a}$，即 $a\leqslant \dfrac 32$；<br/>综上所述，$a$ 的取值范围是 $\left[\dfrac 34,\dfrac 32\right]$． 备注2