如图,设椭圆 $C:\dfrac{x^2}{a^2}+ \dfrac{y^2}{b^2}= 1\left({a > b > 0}\right)$,动直线 $l$ 与椭圆 $C$ 只有一个公共点 $P$,且点 $P$ 在第一象限.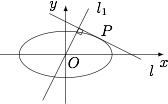

【难度】
【出处】
2014年高考浙江卷(理)
【标注】
-
已知直线 $l$ 的斜率为 $k$,用 $a,b,k$ 表示点 $P$ 的坐标;标注答案点 $P$ 的坐标为 $\left(\dfrac{-a^2k}{\sqrt{a^2k^2+b^2}},\dfrac{b^2}{\sqrt{a^2k^2+b^2}}\right)$解析设 $P(x_0,y_0)$,则 $P$ 点可以用方程$$\dfrac{(x-x_0)^2}{a^2}+\dfrac{(y-y_0)^2}{b^2}=0$$表示,于是在 $P$ 点与椭圆 $C$ 形成的交点曲线系$$\dfrac{(x-x_0)^2}{a^2}+\dfrac{(y-y_0)^2}{b^2}+\lambda\cdot\left(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}-1\right)=0$$中,令 $\lambda=-1$,则得到切线 $l:\dfrac{x_0x}{a^2}+\dfrac{y_0y}{b^2}=1$.因此由$$\begin{cases} -\dfrac{b^2x_0}{a^2y_0}=k,\\ \dfrac{x_0^2}{a^2}+\dfrac{y_0^2}{b^2}=1,\end{cases}$$解得$$\begin{cases} x_0=\dfrac{-a^2k}{\sqrt{a^2k^2+b^2}},\\ y_0=\dfrac{b^2}{\sqrt{a^2k^2+b^2}}.\end{cases}$$因此点 $P$ 的坐标为 $\left(\dfrac{-a^2k}{\sqrt{a^2k^2+b^2}},\dfrac{b^2}{\sqrt{a^2k^2+b^2}}\right)$.
-
若过原点 $O$ 的直线 ${l_1}$ 与 $l$ 垂直,证明:点 $P$ 到直线 ${l_1}$ 的距离的最大值为 $a-b$.标注答案略解析根据题意,直线 $l_1:x+ky=0$,因此点 $P$ 到直线 $l_1$ 的距离为\[\begin{split} \dfrac{|x_0+ky_0|}{\sqrt{1+k^2}}&=\dfrac{\left|\dfrac{-a^2k}{\sqrt{a^2k^2+b^2}}+\dfrac{b^2k}{\sqrt{a^2k^2+b^2}}\right|}{\sqrt{1+k^2}}\\
&=\dfrac{a^2-b^2}{\sqrt{a^2+b^2+a^2k^2+\dfrac{b^2}{k^2}}}\\
&\leqslant \dfrac{a^2-b^2}{\sqrt{a^2+b^2+2ab}}\\
&=a-b,\end{split}\]等号当且仅当 $k=-\sqrt{\dfrac ba}$ 时取得(因为 $P$ 点在第一象限).因此点 $P$ 到直线 $l_1$ 的距离的最大值为 $a-b$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2