设 $\{a,b\}$，$\{c,d\}$ 分别为两个矩形的长和宽，且 $a<c<d<b$，$ab<cd$．证明：可将第一个矩形放入第二个矩形内部的充要条件是$$(b^2-a^2)^2 \leqslant (bd-ac)^2+(bc-ad)^2.$$
【难度】
【出处】
2014年中国人民大学财经学院金融学与数学实验班选拔试题
【标注】
【答案】
略
【解析】
可将第一个矩形放入第二个矩形内部的充要条件是存在 $\theta \in \left(0, \dfrac {\pi}{2}\right)$，使得\begin{eqnarray}\begin{cases}a\sin\theta+b\cos\theta \leqslant c, \\b\sin\theta+a\cos\theta \leqslant d .\end{cases}\end{eqnarray}设 $x=\cos\theta$，$y=\sin\theta$，则 $(1)$ 式成立的充要条件为存在 $x,y \in (0,1)$，使得\begin{eqnarray}\begin{cases} bx+ay \leqslant c ,\\ax+by \leqslant d ,\\x^2+y^2=1.\end{cases} \end{eqnarray}如图，设直线 $\dfrac{x}{c/b}+\dfrac{y}{c/a}=1$ 与直线 $\dfrac{x}{d/a}+\dfrac{y}{d/b}=1$ 与坐标轴的交点分别为 $A$、$B$ 和 $C$、$D$，两条直线的交点为 $E$，则由两个不等式限制的区域为四边形 $OAEC$．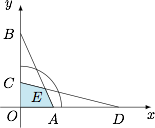
注意到这两条直线的截距均分居 $1$ 的两侧，因此条件组 $(2)$ 有解的充要条件是交点 $E$ 不在圆 $x^2+y^2=1$ 的内部．联立直线方程求得 $E\left(\dfrac {bc-ad}{b^2-a^2},\dfrac {bd-ac}{b^2-a^2}\right)$，于是问题的解为$$(b^2-a^2)^2 \leqslant (bd-ac)^2+(bc-ad)^2.$$
注意到这两条直线的截距均分居 $1$ 的两侧，因此条件组 $(2)$ 有解的充要条件是交点 $E$ 不在圆 $x^2+y^2=1$ 的内部．联立直线方程求得 $E\left(\dfrac {bc-ad}{b^2-a^2},\dfrac {bd-ac}{b^2-a^2}\right)$，于是问题的解为$$(b^2-a^2)^2 \leqslant (bd-ac)^2+(bc-ad)^2.$$
答案
解析
备注
