$P$ 为椭圆 $C:\dfrac{x^2}3+\dfrac{y^2}2=1$ 上一动点,过 $P$ 作圆 $x^2+y^2=1$ 的两条切线分别交椭圆于 $A,B$ 两点,再过 $A,B$ 分别作圆 $O$ 的另一条切线 $AQ,BQ$,它们交于点 $Q$.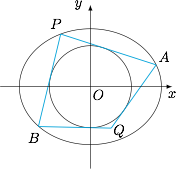

【难度】
【出处】
无
【标注】
-
求动点 $Q$ 的轨迹方程;标注答案$\dfrac{x^2}{\left(\dfrac{33\sqrt 3}{47}\right)^2}+\dfrac{y^2}{\left(\dfrac{37\sqrt 2}{47}\right)^2}=1$解析设 $P$ 点的坐标为 $\left(\sqrt 3\cos\theta,\sqrt 2\sin\theta\right)$,$PA,PB,QA,QB$ 的斜率分别是 $k_1,k_2,k_3,k_4$.设过点 $P$ 的直线方程为$$y-\sqrt 2\sin\theta=k\left(x-\sqrt 3\cos\theta\right),$$则该直线与圆 $x^2+y^2=1$ 相切,即$$\dfrac{\left|\sqrt 2\sin\theta-\sqrt 3k\cos\theta\right|}{\sqrt{1+k^2}}=1,$$也即$$\left(3\cos^2\theta-1\right)k^2-2\sqrt 6\sin\theta\cos\theta\cdot k+2\sin^2\theta-1=0,$$于是$$k_1+k_2=\dfrac{2\sqrt 6\sin\theta\cos\theta}{3\cos^2\theta-1}=\dfrac{2\sqrt 6\sin 2\theta}{3\cos 2\theta+1},k_1k_2=\dfrac{2\sin^2\theta-1}{3\cos^2\theta-1}=\dfrac{-2\cos 2\theta}{3\cos 2\theta+1},$$也即$$\cos 2\theta=\dfrac{-k_1k_2}{3k_1k_2+2}, \sin 2\theta=\dfrac{k_1+k_2}{3\sqrt 6k_1k_2+2\sqrt 6}.$$这样我们就有$$\left(\dfrac{-k_1k_2}{3k_1k_2+2}\right)^2+\left(\dfrac{k_1+k_2}{3\sqrt 6k_1k_2+2\sqrt 6}\right)^2=1,$$整理,得$$48k_1^2k_2^2-\left(k_1^2+k_2^2\right)+70k_1k_2+24=0.$$上式中将 $\left(k_1,k_2\right)$ 换成 $\left(k_1,k_3\right)$,$\left(k_2,k_4\right)$ 依然成立,因此有 $k_2,k_3$ 是关于 $k$ 的方程$$\left(48k_1^2-1\right)k^2+70k_1k+24-k_1^2=0$$的两个根,而 $k_1,k_4$ 是关于 $k$ 的方程$$\left(48k_2^2-1\right)k^2+70k_2k+24-k_2^2=0$$的两个根.于是$$ k_1+k_2+k_3+k_4=\dfrac{-70k_1}{48k_1^2-1}+\dfrac{-70k_2}{48k_2^2-1}, k_1k_2k_3k_4=\dfrac{24-k_1^2}{48k_1^2-1}\cdot \dfrac{24-k_2^2}{48k_2^2-1},$$化简,并注意利用$$48k_1^2k_2^2-\left(k_1^2+k_2^2\right)+70k_1k_2+24=0$$可得$$ k_3+k_4=\dfrac{-1221\left(k_1+k_2\right)}{3360k_1k_2+1151},k_3k_4=\dfrac{1151k_1k_2+1680}{3360k_1k_2+1151},$$进而$$k_3+k_4=\dfrac{2242\sqrt 6\sin 2\theta}{3267\cos 2\theta-1151}, k_3k_4=\dfrac{-\left(2738\cos 2\theta+1680\right)}{3267\cos 2\theta-1151},$$因此 $k_3,k_4$ 是关于 $k$ 的方程$$\left(3267\cos 2\theta-1151\right)k^2-2442\sqrt 6\sin 2\theta\cdot k+2738\cos 2\theta-1680=0,$$也即$$\left(\dfrac{3267}{2209}\cos^2\theta-1\right)k^2-\dfrac{2442\sqrt 6}{2209}\sin\theta\cos\theta\cdot k+\dfrac{2738}{2209}\sin^2\theta-1=0$$的两根.与处理 $k_1,k_2$ 类似,我们有$$\dfrac{\left|\dfrac{37\sqrt 2}{47}\sin\theta-\dfrac{33\sqrt 3}{47}\cos\theta\right|}{\sqrt{1+k^2}}=1,$$于是点 $Q$ 的轨迹方程为$$\dfrac{x^2}{\left(\dfrac{33\sqrt 3}{47}\right)^2}+\dfrac{y^2}{\left(\dfrac{37\sqrt 2}{47}\right)^2}=1.$$经验证,当 $PA,PB,QA,QB$ 中有斜率不存在的情形时,对应的 $Q$ 点仍然满足上述方程,因此所求的 $Q$ 点的轨迹方程为$$\dfrac{x^2}{\left(\dfrac{33\sqrt 3}{47}\right)^2}+\dfrac{y^2}{\left(\dfrac{37\sqrt 2}{47}\right)^2}=1.$$
-
求四边形 $PAQB$ 的面积的取值范围(保留到小数点后 $4$ 位).标注答案$[4.1228,4.2894]$解析设 $P(\sqrt 3\cos\theta,\sqrt 2\sin\theta)$,由第 $(1)$ 问知 $Q\left(-\dfrac {33\sqrt 3}{47}\cos\theta,-\dfrac {37\sqrt 2}{47}\sin\theta\right)$.于是由两点间距离公式得到$$PQ=\dfrac 1{47}\sqrt{19200\cos^2\theta+14112\sin^2\theta}.$$又由第 $(1)$ 问知 $k_1,k_2$ 满足$$(\sqrt 2\sin\theta-\sqrt 3\cos\theta\cdot k_i)^2=1+k_i^2,i=1,2,$$联立直线 $PA,PB$ 与椭圆的方程可以得到点 $A,B$ 的坐标分别为$$A\left(\dfrac {3k_1^2-3}{(3k_1^2+2)\sqrt 3\cos\theta},\dfrac {2-4k_1^2}{(3k_1^2+2)\sqrt 2\sin\theta}\right),B\left(\dfrac {3k_2^2-3}{(3k_2^2+2)\sqrt 3\cos\theta},\dfrac {2-4k_2^2}{(3k_2^2+2)\sqrt 2\sin\theta}\right),$$从而得到 $AB$ 的长度为$$AB=\dfrac{|k_1^2-k_2^2|\sqrt{\dfrac{75\sin^2\theta+98\cos^2\theta}{\sin^2\theta\cos^2\theta}}}{9k_1^2k_2^2+6k_1^2+6k_2^2+4}.$$结合第 $(1)$ 问中 $k_1,k_2$ 是方程$$\left(3\cos^2\theta-1\right)k^2-2\sqrt 6\sin\theta\cos\theta\cdot k+2\sin^2\theta-1=0$$的两个根,可以将 $AB$ 长度化简为$$AB=\dfrac {2\sqrt 6\sqrt{75\sin^2\theta+98\cos^2\theta}\cdot\sqrt{8\sin^2\theta+12\cos^2\theta-4}}{12\cos^2\theta-12\sin^2\theta+37}.$$同时直线 $PQ,AB$ 的斜率分别为\[\begin{split} k_{PQ}=&\dfrac {\sqrt 2\sin\theta+\dfrac {37\sqrt{2}}{47}\sin\theta}{\sqrt 3\cos\theta+\dfrac {33\sqrt 3}{47}\cos\theta}=\dfrac {21\sqrt 2\sin\theta}{20\sqrt 3\cos\theta},\\k_{AB}=&-\dfrac{14\sqrt 3\cos\theta}{15\sqrt 2\sin\theta}.\end{split}.\]于是我们得到直线 $AB$ 与 $PQ$ 的夹角 $\varphi$ 的正切值$$\tan\varphi=\left|\dfrac {k_{AB}-k_{PQ}}{1+k_{AB}k_{PQ}}\right|=\dfrac {35(3\sin^2\theta+4\cos^2\theta)}{\sqrt 6|\sin\theta\cos\theta|}.$$于是我们得到四边形 $PAQB$ 的面积\[\begin{split} S=&\dfrac 12\cdot PQ\cdot AB\cdot \sin\varphi\\=&\dfrac {70\sqrt 6}{47}\cdot\dfrac {(3+\cos^2\theta)\sqrt{(\cos^2\theta+1)(23\cos^2\theta+75)(5088\cos^2\theta+14112)}}{(24\cos^2\theta+25)\sqrt{1219\cos^4\theta+7356\cos^2\theta+11025}}\\=&\dfrac{1680}{47}\cdot\dfrac{(3+t)\sqrt{t+1}}{24t+25}.\end{split}\]其中 $t=\cos^2\theta\in[0,1]$.再令 $\sqrt{t+1}=x\in[1,\sqrt 2]$,研究函数$$f(x)=\dfrac{x(x^2+2)}{24x^2+1},x\in [1,\sqrt 2]$$的最值.因为$$f'(x)=\dfrac {24x^4-45x^2+2}{(24x^2+1)^2},$$所以 $f'(x)$ 在 $[1,\sqrt 2]$ 上有零点 $x_0=\sqrt{\dfrac {45+\sqrt{1833}}{48}}$,得到 $f(x)$ 在 $[1,x_0]$ 上单调递减,在 $[x_0,\sqrt 2]$ 上单调递增.
又因为$$f(1)=\dfrac {1008}{235}>f(\sqrt 2)=\dfrac {960\sqrt 2}{329},$$所以 $f(x)\in [f(x_0),f(1)]$,从而得到 $S$ 的最大值为$$\dfrac{1680}{47}f(1)=\dfrac{1680}{47}\cdot\dfrac {1008}{235}\approx 4.2894,$$最小值为$$\dfrac{1680}{47}\cdot f(x_0)\approx 4.1228.$$所以我们得到面积 $S$ 的取值范围约为 $[4.1228,4.2894]$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2