已知函数 $f\left(x\right)=\dfrac{ax}{\left(x+r\right)^2}$($a>0$,$r>0$).
【难度】
【出处】
2015年高考安徽卷(文)
【标注】
-
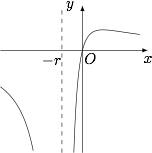
求 $f\left(x\right)$ 的定义域,并讨论 $f\left(x\right)$ 的单调性;标注答案$f(x)$ 的定义域为 $(-\infty ,-r)\cup (-r,+\infty )$,在 $(-\infty ,-r)$ 和 $(r,+\infty )$ 上单调递减,在 $(-r,r)$ 上单调递增解析函数 $f(x)$ 的定义域为 $(-\infty ,-r)\cup (-r,+\infty )$,导函数$$f'(x)=-\dfrac{a(x+r)(x-r)}{(x+r)^4},$$于是函数 $f(x)$ 在 $(-\infty ,-r)$ 上单调递减,在 $(-r,r)$ 上单调递增,在 $(r,+\infty )$ 上单调递减,如图.
-
若 $\dfrac ar=400$,求 $f\left(x\right)$ 在 $\left(0,+\infty\right)$ 内的极值.标注答案在 $x=r$ 处取得极大值 $100$解析根据第 $(1)$ 小题的结果,函数 $f(x)$ 在 $x=r$ 处取得极大值$$f(r)=\dfrac{ar}{(2r)^2}=\dfrac 14\cdot\dfrac ar=100.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2