题目 已知椭圆 $x^2+2y^2=1$，过原点的两条直线 $l_1$ 和 $l_2$ 分别与椭圆交于点 $A,B$ 和 $C,D$．记 $\triangle AOC$ 的面积为 $S$． 问题1 设 $A(x_1,y_1)$，$C(x_2,y_2)$，用 $A,C$ 的坐标表示点 $C$ 到直线 $l_1$ 的距离，并证明 $S=\dfrac12|x_1y_2-x_2y_1|$； 答案1 $\dfrac{|x_1y_2-x_2y_1|}{\sqrt{x_1^2+y_1^2}}$ 解析1 直线 $l_1$ 的方程为 $y_1x-x_1y=0$，因此点 $C$ 到直线 $l_1$ 的距离$$d=\dfrac{|x_1y_2-x_2y_1|}{\sqrt{x_1^2+y_1^2}},$$进而$$S=\dfrac 12\cdot d\cdot |OA|=\dfrac 12\cdot \dfrac{|x_1y_2-x_2y_1|}{\sqrt{x_1^2+y_1^2}}\cdot \sqrt{x_1^2+y_1^2}=\dfrac 12|x_1y_2-x_2y_1|.$$因此原命题得证． 备注1 问题2 设 $l_1:y=kx$，$C\left(\dfrac{\sqrt3}{3},\dfrac{\sqrt3}{3}\right)$，$S=\dfrac13$，求 $k$ 的值； 答案2 $-1$ 或 $-\dfrac 15$ 解析2 联立直线 $l_1$ 的方程与椭圆方程，得 $x_1^2=\dfrac 1{1+2k^2}$．因此由第 $(1)$ 小题的结果可得$$S=\dfrac 12|x_1y_2-x_2y_1|=\dfrac 12\left|\dfrac{\sqrt 3}3\cdot x_1-\dfrac{\sqrt 3}3\cdot kx_1\right|=\dfrac{\sqrt 3}6\cdot\sqrt{\dfrac{(k-1)^2}{2k^2+1}},$$又根据题意 $S=\dfrac 13$，从而解得 $k=-1$ 或 $k=-\dfrac 15$． 备注2 问题3 设 $l_1$ 与 $l_2$ 的斜率之积为 $m$，求 $m$ 的值，使得无论 $l_1$ 与 $l_2$ 如何变动，面积 $S$ 保持不变． 答案3 $-\dfrac 12$ 解析3 在仿射变换 $\begin{cases} x'=x,\\y'=\sqrt 2y\end{cases}$ 下，椭圆 $x^2+2y^2=1$ 变为圆 $x'^2+y'^2=1$，如图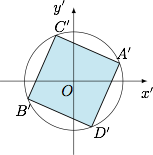．<img src="/static/images/6bb274c95b0c98be4631d638e8d292d1.png" class="img-responsive" />直线 $l_1$ 与 $l_2$ 仿射变换后的直线 $l_1'$ 与 $l_2'$ 的斜率之积为 $2m$，同时 $\triangle AOC$ 仿射变换后成为 $\triangle A'OC'$，其面积 $S'=\sqrt 2S$ 保持不变．<br/>由于 $\triangle A'OC'$ 是腰长为 $1$ 的等腰三角形，于是其面积$$S'=\dfrac 12\cdot\sin\angle A'OC'\cdot |OA'|^2=\dfrac 12\cdot \sin\angle A'OC',$$因此 $\angle A'OC'$ 保持不变．<br/>当 $2m=-1$ 即 $m=-\dfrac 12$ 时，$\angle A'OC'$ 恒为直角，保持不变，符合题意；<br/>当 $2m\neq -1$ 时，显然 $m\neq 0$（否则必然有一条直线为 $x$ 轴，显然不符合题意）．设直线 $l_1'$ 与 $l_2'$ 的斜率分别为 $k,\dfrac {2m}{k}$，则$$|\tan\angle A'OC'|=\left|\dfrac{k-\dfrac{2m}k}{1+k\cdot\dfrac{2m}k}\right|=\left|\dfrac{k-\dfrac{2m}k}{1+2m}\right|$$不为定值，不符合题意．<br/>综上所述，$m$ 的值为 $-\dfrac 12$ 时，无论 $l_1$ 和 $l_2$ 如何变动，面积 $S$ 保持不变． 备注3