• 方法

  >

  思考方式

  >

  信息迁移
• 知识点

  >

  函数

  >

  常见初等函数

  >

  三角函数

略

函数 $h(x)$ 的定义域为 $\mathbb R$，而\[\begin{split} \cos h(x+6\pi)&=\cos\left[(x+6\pi)+\sin\dfrac{x+6\pi}3\right]\\
&=\cos\left[x+\sin\left(\dfrac x3+2\pi\right)\right]\\
&=\cos\left(x+\sin\dfrac x3\right)\\
&=\cos h(x),\end{split}\]从而根据余弦周期函数的定义，$h(x)$ 是以 $6\pi$ 为余弦周期的余弦周期函数．

• 知识点

  >

  函数

  >

  函数的图象与性质

  >

  函数的零点

略

由函数 $f(x)$ 的值域为 $\mathbb{R}$ 知，对任意 $c\in[f(a),f(b)]$，存在 $x_{0}\in\mathbb{R}$，使得 $f(x_{0})=c\in [f(a),f(b)]$，由 $f(x)$ 单调递增知，$x_{0}\in [a,b]$，因此原命题得证．

• 题型

  >

  三角

  >

  解三角方程与不等式
• 知识点

  >

  函数

  >

  函数的图象与性质

  >

  函数的零点

略

若 $u_0+T$ 为方程 $\cos f(x)=1$ 在 $[T,2T]$ 上的解，则根据余弦周期函数的定义，有$$\cos f(u_0)=\cos f(u_0+T)=1,$$且 $u_0\in[0,T]$，于是充分性得证．
反之，若 $u_0$ 为方程 $\cos f(x)=1$ 在 $[0,T]$ 上的解，则根据余弦周期函数的定义，有$$\cos f(u_0+T)=\cos f(u_0)=1,$$且 $u_0+T\in[T,2T]$，于是必要性得证．
综上所述，“$u_0$ 为方程 $\cos f\left(x\right)=1$ 在 $\left[0,T\right]$ 上的解”的充要条件是“$u_0+T$ 为方程 $\cos f\left(x\right)=1$ 在 $\left[T,2T\right]$ 上的解”，如图．
接下来证明 $\forall x\in[0,T],f(x+T)=f(x)+f(T)$．
函数 $y=\cos f(x)$ 可以看作是函数 $y=\cos t$ 和函数 $t=f(x)$ 的复合函数，如图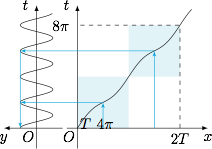．根据第 $(2)$ 小题的结论，存在 $x_1,x_2,x_3$ 满足 $0<x_1<x_2<x_3<T$，使得 $f(x_k)=k\pi$，其中 $k=1,2,3$．为方便叙述，记 $x_0=0$，$x_4=T$．
当 $x\in [x_0,x_1]$ 时，函数 $y=\cos f(x)$ 是单调递减函数，因此每一个自变量的值 $x$ 都唯一对应一个函数值 $\cos f(x)$．此时 $x+T\in [x_0+T,x_1+T]$，且根据余弦周期函数的定义，有$$\cos f(x+T)=\cos f(x).$$特别地，有 $f(x_0+T)=f(T)=4\pi$，且 $\cos f(x_1+T)=\cos f(x_1)=-1$．
下面证明函数 $y=\cos f(x)$ 在区间 $[x_0+T,x_1+T]$ 上单调递减：
任取 $\alpha,\beta\in [x_{0}+T,x_{1}+T],\alpha<\beta$，有 $x_{0}\leqslant \alpha-T<\beta-T\leqslant x_{1}$，由函数 $y=\cos f(x)$ 在 $[x_{0},x_{1}]$ 上单调递减知 $\cos f(\alpha -T)>\cos f(\beta -T)$，即 $\cos f(\alpha)>\cos f(\beta)$，从而得到函数 $y=\cos f(x)$ 在区间 $[x_0+T,x_1+T]$ 上单调递减．
综合以上两点，结合余弦函数的单调性，我们有 $f(x_1+T)=5\pi$，且对任意 $x\in[x_0,x_1]$，均有 $f(x+T)=f(x)+4\pi$，命题成立．
类似地，可以证明当 $x$ 在区间 $[x_1,x_2],[x_2,x_3],[x_3,x_4]$ 上时命题均成立，因此原命题得证．