已知边长为 $1$ 的正三角形 $ABC$ 的中心为 $O$，在 $\triangle ABC$ 的内切圆上取一点 $P$，将 $\overrightarrow{PA},\overrightarrow{PB},\overrightarrow{PC},\overrightarrow{PO}$ 四个向量分为两组 $\{\overrightarrow a,\overrightarrow b\}$ 和 $\{\overrightarrow c,\overrightarrow d\}$，把 $\left(\overrightarrow a+\overrightarrow b\right)\cdot \left(\overrightarrow c+\overrightarrow d\right)$ 的取值集合记为 $K$，则对于一切 $P$，有 \((\qquad)\)
【难度】
【出处】
2017年清华大学THUSSAT附加学科测试数学部分（二测）
【标注】
【答案】
ABC
【解析】
记 $AB$ 的中点为 $M$，$CO$ 的中点为 $N$，由正三角形的性质知 $MN$ 为内切圆 $O$ 的直径，如图：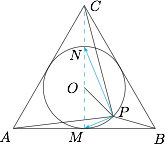
从而有\[\begin{split}\left(\overrightarrow{PA}+\overrightarrow{PB}\right)\cdot \left(\overrightarrow{PC}+\overrightarrow{PO}\right)&=4\overrightarrow{PM}\cdot\overrightarrow{PN}=0.\end{split}\]
从而有\[\begin{split}\left(\overrightarrow{PA}+\overrightarrow{PB}\right)\cdot \left(\overrightarrow{PC}+\overrightarrow{PO}\right)&=4\overrightarrow{PM}\cdot\overrightarrow{PN}=0.\end{split}\]
题目
答案
解析
备注
