已知六边形 $A{C_1}B{A_1}C{B_1}$ 中，
① $A{C_1} = A{B_1}$，$B{C_1} = B{A_1}$，$C{A_1} = C{B_1}$；
② $\angle A + \angle B + \angle C = \angle {A_1} + \angle {B_1} + \angle {C_1}$．
求证：$\triangle ABC$ 面积是六边形 $A{C_1}B{A_1}C{B_1}$ 的一半．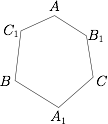
① $A{C_1} = A{B_1}$，$B{C_1} = B{A_1}$，$C{A_1} = C{B_1}$；
② $\angle A + \angle B + \angle C = \angle {A_1} + \angle {B_1} + \angle {C_1}$．
求证：$\triangle ABC$ 面积是六边形 $A{C_1}B{A_1}C{B_1}$ 的一半．
【难度】
【出处】
2008年北京大学自主招生保送生测试
【标注】
【答案】
略
【解析】
因为六边形的内角和为 $720^\circ $，所以$$\angle A + \angle B + \angle C = \angle {A_1} + \angle {B_1} + \angle {C_1} = 360^\circ. $$如图，
将 $\triangle A{C_1}B$ 旋转到 $\triangle A{B_1}P$，将 $\triangle CB{A_1}$ 旋转到 $\triangle CP{B_1}$，
则$$AB = AP,BC = PC,AC = AC,$$于是$$\triangle ABC\cong\triangle APC,$$因此 $\triangle ABC$ 面积是六边形 $A{C_1}B{A_1}C{B_1}$ 的一半．
将 $\triangle A{C_1}B$ 旋转到 $\triangle A{B_1}P$，将 $\triangle CB{A_1}$ 旋转到 $\triangle CP{B_1}$，则$$AB = AP,BC = PC,AC = AC,$$于是$$\triangle ABC\cong\triangle APC,$$因此 $\triangle ABC$ 面积是六边形 $A{C_1}B{A_1}C{B_1}$ 的一半．
答案
解析
备注
